


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-7-2019
Date: 29-9-2019
Date: 14-8-2019
|
There are (at least) two mathematical constants associated with Theodorus. The first Theodorus's constant is the elementary algebraic number 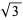 , i.e., the square root of 3. It has decimal expansion
, i.e., the square root of 3. It has decimal expansion
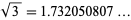 |
(1) |
(OEIS A002194) and is named after Theodorus, who proved that the square roots of the integers from 3 to 17 (excluding squares 4, 9,and 16) are irrational (Wells 1986, p. 34). The space diagonal of a unit cube has length 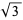 .
.
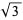 has continued fraction [1, 1, 2, 1, 2, 1, 2, ...] (OEIS A040001). In binary, it is represented by
has continued fraction [1, 1, 2, 1, 2, 1, 2, ...] (OEIS A040001). In binary, it is represented by
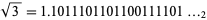 |
(2) |
(OEIS A004547).
Another constant sometimes known as the constant of Theodorus is the slope of a continuous analog of the discrete Theodorus spiral due to Davis (1993) at the point 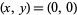 , given by
, given by
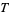 |
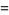 |
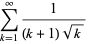 |
(3) |
 |
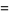 |
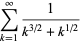 |
(4) |
 |
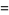 |
![1/2-sum_(k=1)^(infty)(-1)^k[zeta(k+1/2)-1]](http://mathworld.wolfram.com/images/equations/TheodorussConstant/Inline13.gif) |
(5) |
 |
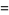 |
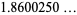 |
(6) |
(OEIS A226317; Finch 2009), where 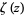 is the Riemann zeta function.
is the Riemann zeta function.
REFERENCES:
Davis, P. J. Spirals from Theodorus to Chaos. Wellesley, MA: A K Peters, 1993.
Finch, S. "Constant of Theodorus." http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.440.3922&rep=rep1&type=pdf.
Gautschi, W. "The Spiral of Theodorus, Numerical Analysis, and Special Functions."https://www.cs.purdue.edu/homes/wxg/slidesTheodorus.pdf.
Jones, M. F. "Approximations to the Square Roots of the Primes Less Than 100." Math. Comput. 22, 234-235, 1968.
Sloane, N. J. A. Sequences A002194/M4326, A004547, A040001, and A226317 in "The On-Line Encyclopedia of Integer Sequences."
Uhler, H. S. "Approximations Exceeding 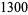 Decimals for
Decimals for 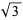 ,
, 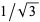 ,
, 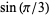 , and Distribution of Digits in Them." Proc. Nat. Acad. Sci. USA 37, 443-447, 1951.
, and Distribution of Digits in Them." Proc. Nat. Acad. Sci. USA 37, 443-447, 1951.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 34-35, 1986.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|