


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-5-2019
Date: 22-8-2019
Date: 24-6-2019
|
Let 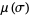 be the least upper bound of the numbers
be the least upper bound of the numbers 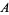 such that
such that 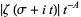 is bounded as
is bounded as 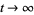 , where
, where 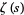 is the Riemann zeta function. Then the Lindelöf hypothesis states that
is the Riemann zeta function. Then the Lindelöf hypothesis states that 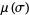 is the simplest function that is zero for
is the simplest function that is zero for 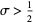 and
and 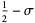 for
for 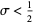 .
.
The Lindelöf hypothesis is equivalent to the hypothesis that 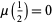 (Edwards 2001, p. 186).
(Edwards 2001, p. 186).
Backlund (1918-1919) proved that the Lindelöf hypothesis is equivalent to the statement that for every 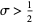 , the number of roots in the rectangle
, the number of roots in the rectangle ![{T<=I[s]<=T+1,sigma<=R[s]<=1}](http://mathworld.wolfram.com/images/equations/LindelofHypothesis/Inline12.gif) grows less rapidly than
grows less rapidly than 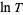 as
as 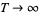 (Edwards 2001, p. 188).
(Edwards 2001, p. 188).
REFERENCES:
Backlund, R. "Über die Beziehung zwischen Anwachsen und Nullstellen der Zeta-Funktion." Ofversigt Finka Vetensk. Soc. 61, No. 9, 1918-1919.
Edwards, H. M. Riemann's Zeta Function. New York: Dover, 2001.
Lindelöf, E. "Quelque remarques sur la croissance de la fonction 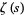 ." Bull. Sci. Math. 32, 341-356, 1908.
." Bull. Sci. Math. 32, 341-356, 1908.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|