


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-3-2019
Date: 24-3-2019
Date: 25-4-2019
|

The Euler polynomial 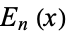 is given by the Appell sequence with
is given by the Appell sequence with
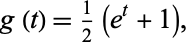 |
(1) |
giving the generating function
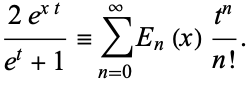 |
(2) |
The first few Euler polynomials are
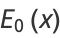 |
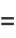 |
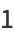 |
(3) |
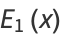 |
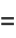 |
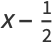 |
(4) |
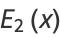 |
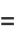 |
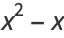 |
(5) |
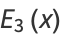 |
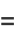 |
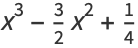 |
(6) |
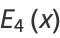 |
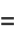 |
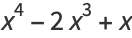 |
(7) |
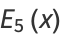 |
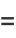 |
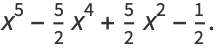 |
(8) |
Roman (1984, p. 100) defines a generalization 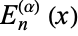 for which
for which 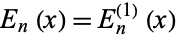 . Euler polynomials are related to the Bernoulli numbers by
. Euler polynomials are related to the Bernoulli numbers by
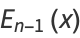 |
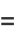 |
![(2^n)/n[B_n((x+1)/2)-B_n(x/2)]](http://mathworld.wolfram.com/images/equations/EulerPolynomial/Inline24.gif) |
(9) |
 |
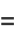 |
![2/n[B_n(x)-2^nB_n(x/2)]](http://mathworld.wolfram.com/images/equations/EulerPolynomial/Inline27.gif) |
(10) |
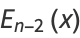 |
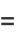 |
![2(n; 2)^(-1)sum_(k=0)^(n-2)(n; k)[(2^(n-k)-1)B_(n-k)B_k(x)],](http://mathworld.wolfram.com/images/equations/EulerPolynomial/Inline30.gif) |
(11) |
where 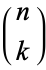 is a binomial coefficient. Setting
is a binomial coefficient. Setting 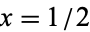 and normalizing by
and normalizing by 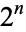 gives the Euler number
gives the Euler number
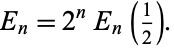 |
(12) |
The first few values of 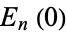 are
are 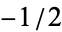 , 0, 1/4,
, 0, 1/4, 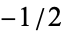 , 0, 17/8, 0, 31/2, 0, .... The terms are the same but with the signs reversed if
, 0, 17/8, 0, 31/2, 0, .... The terms are the same but with the signs reversed if 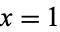 . These values can be computed using the double series
. These values can be computed using the double series
![E_n(0)=2^(-n)sum_(j=1)^n[(-1)^(j+n+1)j^nsum_(k=0)^(n-j)(n+1; k)].](http://mathworld.wolfram.com/images/equations/EulerPolynomial/NumberedEquation4.gif) |
(13) |
The Bernoulli numbers 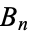 for
for 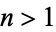 can be expressed in terms of
can be expressed in terms of  by
by
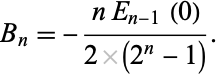 |
(14) |
The Newton expansion of the Euler polynomials is given by
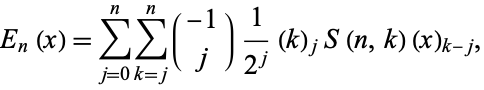 |
(15) |
where 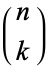 is a binomial coefficient,
is a binomial coefficient, 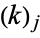 is a falling factorial, and
is a falling factorial, and 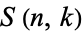 is a Stirling number of the second kind (Roman 1984, p. 101).
is a Stirling number of the second kind (Roman 1984, p. 101).
The Euler polynomials satisfy the identities
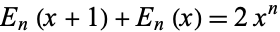 |
(16) |
and
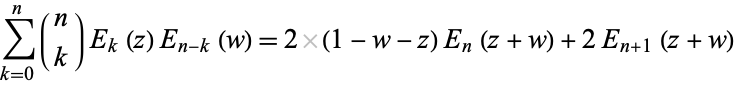 |
(17) |
for 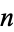 a nonnegative integer.
a nonnegative integer.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula." §23.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 804-806, 1972.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Generalized Zeta Function 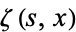 , Bernoulli Polynomials
, Bernoulli Polynomials 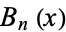 , Euler Polynomials
, Euler Polynomials 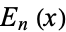 , and Polylogarithms
, and Polylogarithms 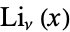 ." §1.2 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 23-24, 1990.
." §1.2 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 23-24, 1990.
Roman, S. "The Euler Polynomials." §4.2.3 in The Umbral Calculus. New York: Academic Press, pp. 100-106, 1984.
Spanier, J. and Oldham, K. B. "The Euler Polynomials 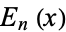 ." Ch. 20 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 175-181, 1987.
." Ch. 20 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 175-181, 1987.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|