Ruffini's rule a shortcut method for dividing a polynomial by a linear factor of the form 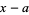 which can be used in place of the standard long division algorithm. This method reduces the polynomial and the linear factor into a set of numeric values. After these values are processed, the resulting set of numeric outputs is used to construct the polynomial quotient and the polynomial remainder.

Note that Ruffini's rule is a special case of the more generalized notion of synthetic division in which the divisor polynomial is a monic linear polynomial. Confusingly, Ruffini's rule is sometimes referred to as synthetic division, thus leading to the common misconception that the scope of synthetic division is significantly smaller than that of the long division algorithm.

For an example of Ruffini's rule, consider 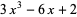 divided by 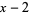. First, if a power of  is missing from the dividend, a term with that power and a zero coefficient must be inserted into the correct position in the polynomial. In this case the 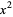 term is missing from the dividend, so  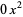must be added between the cubic and linear terms:

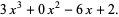(1)

Next, all the variables and their exponents (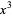, , 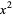) are removed from the dividend, leaving only a list of the dividend's coefficients: 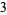, , 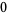, 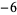and 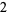. Next, because only the constant term (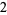) of the linear factor  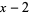is necessary for Ruffini's rule, the divisor is modified into a one-term "sequence" 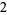. Note that if the divisor were 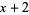, rewriting as  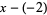would result in a modified divisor sequence of  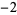instead.

The numbers representing the divisor and the dividend sequences are placed into a division-like configuration:

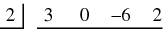
The first number in the dividend (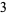) is put into the first position of the result area (below the horizontal line). This number is the coefficient of the  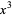term in the original dividend polynomial:

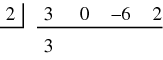
Then this first entry in the result (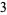) is multiplied by the divisor (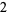) and the product is placed under the next term in the dividend ():

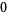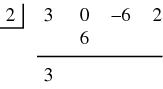
Next the number from the dividend and the result of the multiplication are added together and the sum is put in the next position on the result line:

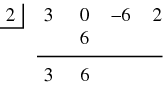
This process is continued for the remainder of the numbers in the dividend:

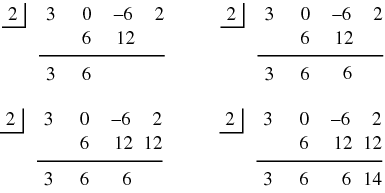
The result is the sequence 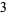, , 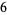, 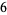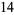. All numbers except the last become the coefficients of the quotient polynomial. Since a cubic polynomial was divided by a linear term, the quotient is a 2nd degree polynomial:

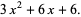(2)

The last entry in the result list (namely, 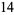) is the remainder. The quotient and remainder can be combined into one expression:

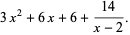(3)

(Note that no division operations were performed to compute the answer to this division problem.)

To verify that this process has worked, one can multiply the quotient by the divisor and add the remainder to obtain the original dividend polynomial:

			(4)
			(5)

Ruffini's rule can be used in conjunction with the polynomial remainder theorem to evaluate a polynomial at a real value. For example, consider the polynomial

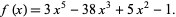(6)

To find the value of 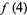, the remainder theorem states that  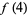is the remainder when  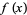is divided by 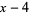. Using Ruffini's rule, one obtains:

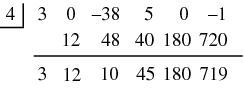
Therefore .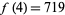

REFERENCES:

Lipschutz, S. Schaum's Outline of Linear Algebra. New York: McGraw-Hill, pp. 326-327, 2000.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Polynomials and Rational Functions." §5.3 in Numerical Recipes in C: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 173-176, 1992. http://www.library.cornell.edu/nr/bookcpdf/c5-3.pdf.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد