Gamma-Modular Function
المؤلف:
Borwein, J. M. and Borwein, P. B
المصدر:
Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
الجزء والصفحة:
...
23-12-2019
1172
Gamma-Modular Function
The modular group Gamma is the set of all transformations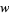 
of the form
where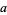 
, 
, 
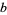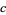, and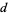 
are integers and 
.
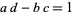A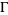 
-modular function is then defined (Borwein and Borwein 1987, p. 114) as a function 
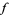that satisfies:
1. 
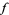is meromorphic in the upper half-plane 
.
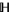2. 
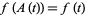for all 
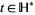, where ![H^*=H union <span style=]()
{iinfty} union Q" src="http://mathworld.wolfram.com/images/equations/Gamma-ModularFunction/Inline13.gif" style="height:15px; width:118px" />.
3. 
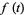tends to a limit (possibly infinite in the sense that 
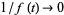) as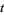 
tends to the vertices of the fundamental region 
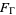where the approach is from within the fundamental region 
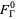. (In the case 
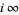, convergence is uniform in ![R[x+iy]](http://mathworld.wolfram.com/images/equations/Gamma-ModularFunction/Inline20.gif)
as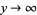 
.) The vertices of the fundamental region are 
, 
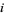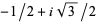and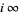 
. Since 
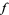is meromorphic in 
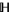, this condition is automatically satisfied at 
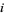and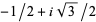 
and need be checked only at 
.
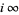REFERENCES:
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
