

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Dragon Curve
المؤلف:
Bulaevsky, J.
المصدر:
"The Dragon Curve or Jurassic Park Fractal." http://ejad.best.vwh.net/java/fractals/jurasic.shtml.
الجزء والصفحة:
...
29-12-2019
1268
Dragon Curve
A dragon curve is a recursive nonintersecting curve whose name derives from its resemblance to a certain mythical creature.
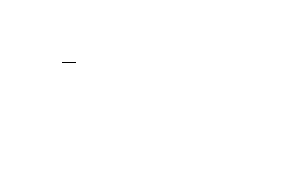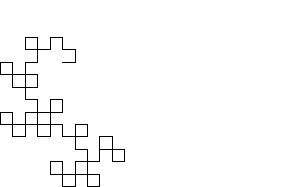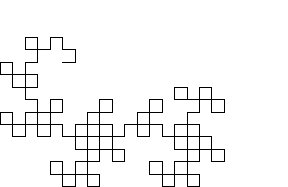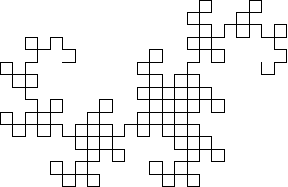
The curve can be constructed by representing a left turn by 1 and a right turn by 0. The first-order curve is then denoted 1. For higher order curves, append a 1 to the end, then append the string of preceding digits with its middle digit complemented. For example, the second-order curve is generated as follows: 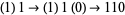 , and the third as
, and the third as 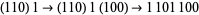 .
.

Continuing gives 110110011100100... (OEIS A014577), which is sometimes known as the regular paperfolding sequence and written with 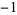 s instead of 0s (Allouche and Shallit 2003, p. 155). A recurrence plot of the limiting value of this sequence is illustrated above.
s instead of 0s (Allouche and Shallit 2003, p. 155). A recurrence plot of the limiting value of this sequence is illustrated above.
Representing the sequence of binary digits 1, 110, 1101100, 110110011100100, ... in octal gives 1, 6, 154, 66344, ...(OEIS A003460; Gardner 1978, p. 216).
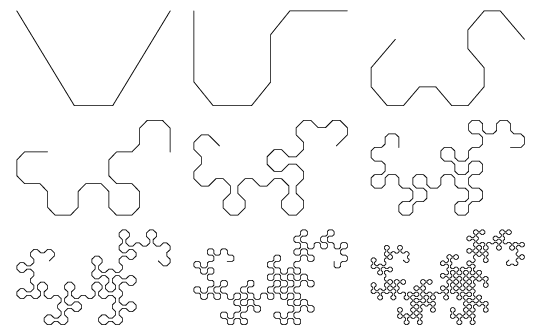
This procedure is equivalent to drawing a right angle and subsequently replacing each right angle with another smaller right angle (Gardner 1978). In fact, the dragon curve can be written as a Lindenmayer system with initial string "FX", string rewriting rules "X" -> "X+YF+", "Y" -> "-FX-Y", and angle 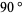 . The dragon curves of orders 1 to 9 are illustrated above, with corners rounded to emphasize the path taken by the curve.
. The dragon curves of orders 1 to 9 are illustrated above, with corners rounded to emphasize the path taken by the curve.
REFERENCES:
Allouche, J.-P. and Mendès France, M. "Automata and Automatic Sequences." In Beyond Quasicrystals (Ed. F. Axel et al.). Berlin: Springer-Verlag, pp. 293-367, 1994.
Allouche, J.-P. and Shallit, J. "Example 5.1.6 (The Regular Paperfolding Sequence)." Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, pp. 155-156, 2003.
Bulaevsky, J. "The Dragon Curve or Jurassic Park Fractal." http://ejad.best.vwh.net/java/fractals/jurasic.shtml.
Charpentier, M. "L-Systems in PostScript." http://www.cs.unh.edu/~charpov/Programming/L-systems/.
Dickau, R. M. "Two-Dimensional L-Systems." http://mathforum.org/advanced/robertd/lsys2d.html.
Dixon, R. Mathographics. New York: Dover, pp. 180-181, 1991.
Dubrovsky, V. "Nesting Puzzles, Part I: Moving Oriental Towers." Quantum 6, 53-57 (Jan.) and 49-51 (Feb.), 1996.
Dubrovsky, V. "Nesting Puzzles, Part II: Chinese Rings Produce a Chinese Monster." Quantum 6, 61-65 (Mar.) and 58-59 (Apr.), 1996.
Gardner, M. Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 207-209 and 215-220, 1978.
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 48-53, 1991.
Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, pp. 66-67, 1983.
Peitgen, H.-O. and Saupe, D. (Eds.). The Science of Fractal Images. New York: Springer-Verlag, p. 284, 1988.
Sloane, N. J. A. Sequences A003460/M4300 and A014577 in "The On-Line Encyclopedia of Integer Sequences."
Vasilyev, N. and Gutenmacher, V. "Dragon Curves." Quantum 6, 5-10, 1995.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 59, 1991.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















