

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Thue-Morse Sequence
المؤلف:
Allouche, J.-P. and Cosnard, M.
المصدر:
"The Komornik-Loreti Constant Is Transcendental." Amer. Math. Monthly 107
الجزء والصفحة:
...
30-12-2019
1685
Thue-Morse Sequence
The Thue-Morse sequence, also called the Morse-Thue sequence or Prouhet-Thue-Morse sequence (Allouche and Cosnard 2000), is one of a number of related sequences of numbers obtained from the parities of the counts of 1's in the binary representation of the nonnegative integers.
The version obtained by directly taking the parities is
 |
(1) |
where 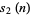 is the binary digit sum. For
is the binary digit sum. For 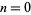 , 1, 2, ..., the first few terms are then given by 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, ... (OEIS A010060; Allouche and Shallit 2003, pp. 15 and 153). An alternate form of the sequence obtained by the taking the binary complement is given by 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, ... (OEIS A010059; Wolfram 2002, p. 890).
, 1, 2, ..., the first few terms are then given by 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, ... (OEIS A010060; Allouche and Shallit 2003, pp. 15 and 153). An alternate form of the sequence obtained by the taking the binary complement is given by 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, ... (OEIS A010059; Wolfram 2002, p. 890).
Interpreting the Thue-Morse sequence as concatenated binary digits gives the Thue-Morse constant.

A recurrence plot of the Thue-Morse sequence is illustrated above.
There is an amazing set of products involving the Thue-Morse sequence {t_n}" src="http://mathworld.wolfram.com/images/equations/Thue-MorseSequence/Inline3.gif" style="height:15px; width:20px" /> given by
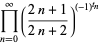 |
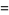 |
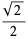 |
(2) |
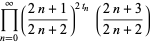 |
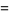 |
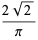 |
(3) |
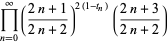 |
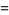 |
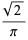 |
(4) |
(Allouche and Shallit 2003, pp. 153 and 204, factor of two typos corrected), the first of which is due to Woods (1978) and Robbins (1979) and is the special case 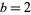 of the digit sum identity due to Sondow (2006).
of the digit sum identity due to Sondow (2006).
Amazingly, the Thue-Morse sequence can be generated from the substitution system
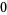 |
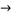 |
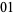 |
(5) |
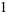 |
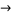 |
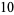 |
(6) |
to obtain
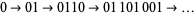 |
(7) |
when starting with 0, and
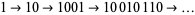 |
(8) |
starting with 1. Interpreting these to sequences as decimal numbers gives the sequences 0, 1, 6, 105, 27030, 1771476585, ... (OEIS A048707) and 1, 2, 9,1 50, 38505, 2523490710, ..., respectively. After the initial generation, each subsequence generation has 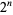 0s and
0s and 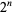 1s.
1s.
Wolfram (2002) provides various pieces of Wolfram Language code that produce the first 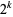 terms of the complemented Thue-Morse sequence 1, 0, 0, 1, 0, 0, 1, ... computed as:
terms of the complemented Thue-Morse sequence 1, 0, 0, 1, 0, 0, 1, ... computed as:
1. A substitution system,
2. The position of the evil numbers, which have an even number of 1's in their binary expansion (OEIS A001969),
3. A generating function, following 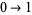 ,
, 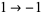 ,
,
4. A cellular automaton (Wolfram 2002, p. 1186),
5. An algebraic generating function,
6. A closed-form expression in terms of a hypergeometric function.
(* 1 *)
Nest[Join[#, 1 - #]&, {1}, k]
(* 2 *)
Table[1 - Mod[DigitCount[n - 1, 2, 1], 2],
{n, 2^k}]
(* 3 *)
(CoefficientList[Product[1 - z^(2^s),
{s, 0, k - 1}], z] + 1)/2
(* 4 *)
Flatten[CellularAutomaton[{69540422, 2, 2},
{{1}, 0}, 2^k - 1, {All, 0}]]
(* 5 *)
Mod[CoefficientList[Series[(1 + Sqrt[(1 - 3 x)/
(1 + x)])/(2 (1 + x)), {x, 0, 2^k - 1}], x], 2]
(* 6 *)
Mod[Table[(-1)^n/2 + (-3)^n Sqrt[Pi] *
Hypergeometric2F1Regularized[3/2, - n, 3/2 - n, - 1/3]/
(4 n!), {n, 0, 2^k - 1}], 2]
Writing the sequence as a power series over the finite field GF(2),
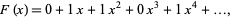 |
(9) |
then 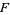 satisfies the quadratic equation
satisfies the quadratic equation
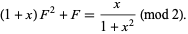 |
(10) |
This equation has two solutions, 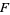 and
and 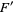 , where
, where 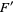 is the complement of
is the complement of 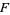 , i.e.,
, i.e.,
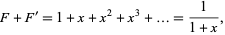 |
(11) |
which is consistent with the formula for the sum of the roots of a quadratic. The equality (10) can be demonstrated as follows. Let (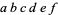 ...) be a shorthand for the power series
...) be a shorthand for the power series
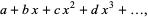 |
(12) |
so 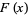 is (0110100110010110...). To get
is (0110100110010110...). To get 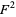 , simply use the rule for squaring power series over GF(2)
, simply use the rule for squaring power series over GF(2)
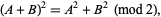 |
(13) |
which extends to the simple rule for squaring a power series
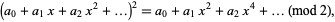 |
(14) |
i.e., space the series out by a factor of 2, (0 1 1 0 1 0 0 1 ...), and insert zeros in the odd places to get
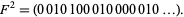 |
(15) |
Then multiply by  (which just adds a zero at the front) to get
(which just adds a zero at the front) to get
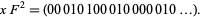 |
(16) |
Adding to 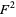 gives
gives
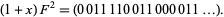 |
(17) |
This is the first term of the quadratic equation, which is the Thue-Morse sequence with each term doubled up. The next term is 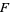 , so we have
, so we have
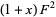 |
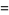 |
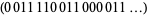 |
(18) |
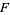 |
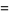 |
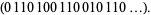 |
(19) |
The sum is the above two sequences XORed together (there are no carries because we're working over GF(2)), giving
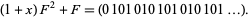 |
(20) |
We therefore have
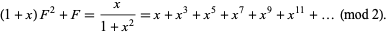 |
(21) |
The Thue-Morse words are overlapfree (Allouche and Shallit 2003, p. 15), and therefore also cubefree on two symbols (Morse and Hedlund 1944). The sequence therefore contains no substrings of the form 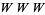 , where
, where 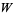 is any word. For example, it does not contain the words 000, 010101 or 010010010. In fact, the following stronger statement is true: the Thue-Morse sequence does not contain any substrings of the form
is any word. For example, it does not contain the words 000, 010101 or 010010010. In fact, the following stronger statement is true: the Thue-Morse sequence does not contain any substrings of the form 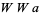 , where
, where 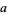 is the first symbol of
is the first symbol of 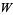 . We can obtain a squarefree sequence on three symbols by doing the following: take the Thue-Morse sequence 0110100110010110... and look at the sequence of words of length 2 that appear: 10 01 10 00 01 11 10 .... Replace 01 by 0, 10 by 1, 00 by 2 and 11 by 2 to get the following: 1012021.... Then this sequence is squarefree (Morse and Hedlund 1944).
. We can obtain a squarefree sequence on three symbols by doing the following: take the Thue-Morse sequence 0110100110010110... and look at the sequence of words of length 2 that appear: 10 01 10 00 01 11 10 .... Replace 01 by 0, 10 by 1, 00 by 2 and 11 by 2 to get the following: 1012021.... Then this sequence is squarefree (Morse and Hedlund 1944).
The Thue-Morse sequence has important connections with the Gray code. Kindermann generates fractal music using the self-similarity of the Thue-Morse sequence.
REFERENCES:
Allouche, J.-P. and Cosnard, M. "The Komornik-Loreti Constant Is Transcendental." Amer. Math. Monthly 107, 448-449, 2000.
Allouche, J.-P. and Shallit, J. "The Ubiquitous Prouhet-Thue-Morse Sequence." In Sequences and Their applications, Proc. SETA'98 (Ed. C. Ding, T. Helleseth, and H. Niederreiter). New York: Springer-Verlag, pp. 1-16, 1999.
Allouche, J.-P. and Shallit, J. "Example 5.1.2 (The Thue-Morse Sequence)." Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, pp. 152-153, 2003.
Goldstein, S.; Kelly, K. A.; and Speer, E. R. "The Fractal Structure of Rarefied Sums of the Thue-Morse Sequence." J. Number Th. 42, 1-19, 1992.
Kindermann, L. "MusiNum--The Music in the Numbers." http://reglos.de/musinum/.
Lothaire, M. (Ed.). Combinatorics on Words. Cambridge, England: Cambridge University Press, 1997.
Morse, M. "Recurrent Geodesics on a Surface of Negative Curvature." Trans. Amer. Math. Soc. 22, 84-100, 1921.
Morse, M. and Hedlund, G. A. "Unending Chess, Symbolic Dynamics, and a Problem in Semigroups." Duke Math. J. 11, 1-7, 1944.
Pickover, C. A. "The Pipes of Papua." Ch. 17 in Wonders of Numbers: Adventures in Mathematics, Mind, and Meaning. Oxford, England: Oxford University Press, pp. 34-38, 2001.
Prouhet, E. "Mémoir sur quelques relations entre les puissances des nombres." C. R. Adad. Sci. Paris Sér. 1 33, 225, 1851.
Robbins, D. "Solution to Problem E2692." Amer. Math. Monthly 86, 394-395, 1979.
Schroeder, M. R. Fractals, Chaos, and Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, 1991.
Sloane, N. J. A. Sequences A010060 and A048707 in "The On-Line Encyclopedia of Integer Sequences."
Sondow, J. "Problem 11222." Amer. Math. Monthly 113, 459, 2006.
Thue, A. "Über unendliche Zeichenreihen." Norske vid. Selsk. Skr. Mat. Nat. Kl. 7, 1-22, 1906. Reprinted in Selected Mathematical Papers of Axel Thue (Ed. T. Nagell). Oslo: Universitetsforlaget, pp. 139-158, 1977.
Thue, A. "Über die gegenseitige Lage gleicher Teile gewisser Zeichenreihen." Norske vid. Selsk. Skr. Mat. Nat. Kl. 1, 1-67, 1912. Reprinted in Selected Mathematical Papers of Axel Thue (Ed. T. Nagell). Oslo: Universitetsforlaget, pp. 413-478, 1977.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 890 and 1092, 2002.
Woods, D. R. "Problem Proposal E2692." Amer. Math. Monthly 85, 48, 1978.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















