
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-12-2020
Date: 15-1-2020
Date: 1-11-2019
|
Let 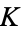 be a number field, then each fractional ideal
be a number field, then each fractional ideal 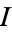 of
of 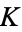 belongs to an equivalence class
belongs to an equivalence class ![[I]](http://mathworld.wolfram.com/images/equations/ClassGroup/Inline4.gif) consisting of all fractional ideals
consisting of all fractional ideals 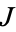 satisfying
satisfying 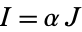 for some nonzero element
for some nonzero element 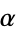 of
of  . The number of equivalence classes of fractional ideals of
. The number of equivalence classes of fractional ideals of  is a finite number, known as the class number of
is a finite number, known as the class number of 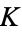 . Multiplication of equivalence classes of fractional ideals is defined in the obvious way, i.e., by letting
. Multiplication of equivalence classes of fractional ideals is defined in the obvious way, i.e., by letting ![[I][J]=[IJ]](http://mathworld.wolfram.com/images/equations/ClassGroup/Inline11.gif) . It is easy to show that with this definition, the set of equivalence classes of fractional ideals form an Abelian multiplicative group, known as the class group of
. It is easy to show that with this definition, the set of equivalence classes of fractional ideals form an Abelian multiplicative group, known as the class group of 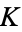 .
.
REFERENCES:
Marcus, D. A. Number Fields, 3rd ed. New York: Springer-Verlag, 1996.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|