For a given 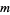, determine a complete list of fundamental binary quadratic form discriminants  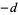such that the class number is given by 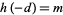. Heegner (1952) gave a solution for 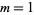, but it was not completely accepted due to a number of apparent gaps. However, subsequent examination of Heegner's proof showed it to be "essentially" correct (Conway and Guy 1996). Conway and Guy (1996) therefore call the nine values of  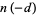having  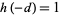where 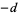 is the binary quadratic form discriminant corresponding to an quadratic fiel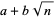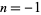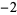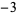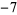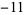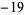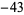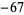d  (, , , , , , , , and 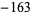; OEIS A003173) the Heegner numbers. The Heegner numbers have a number of fascinating properties.

Stark (1967) and Baker (1966) gave independent proofs of the fact that only nine such numbers exist; both proofs were accepted. Baker (1971) and Stark (1975) subsequently and independently solved the generalized class number problem completely for 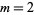. Oesterlé (1985) solved the case 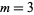, and Arno (1992) solved the case 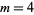. Wagner (1996) solved the cases 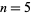, 6, and 7. Arno et al. (1993) solved the problem for odd  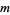satisfying 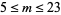. Using extensive computations, Watkins (2004) has solved the problem for all .

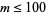REFERENCES:

Arno, S. "The Imaginary Quadratic Fields of Class Number 4." Acta Arith. 40, 321-334, 1992.

Arno, S.; Robinson, M. L.; and Wheeler, F. S. "Imaginary Quadratic Fields with Small Odd Class Number." Dec. 1993. http://www.math.uiuc.edu/Algebraic-Number-Theory/0009/.

Baker, A. "Linear Forms in the Logarithms of Algebraic Numbers. I." Mathematika 13, 204-216, 1966.

Baker, A. "Imaginary Quadratic Fields with Class Number 2." Ann. Math. 94, 139-152, 1971.

Conway, J. H. and Guy, R. K. "The Nine Magic Discriminants." In The Book of Numbers. New York: Springer-Verlag, pp. 224-226, 1996.

Goldfeld, D. M. "Gauss' Class Number Problem for Imaginary Quadratic Fields." Bull. Amer. Math. Soc. 13, 23-37, 1985.

Heegner, K. "Diophantische Analysis und Modulfunktionen." Math. Z. 56, 227-253, 1952.

Heilbronn, H. A. and Linfoot, E. H. "On the Imaginary Quadratic Corpora of Class-Number One." Quart. J. Math. (Oxford) 5, 293-301, 1934.

Ireland, K. and Rosen, M. A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, p. 192, 1990.

Lehmer, D. H. "On Imaginary Quadratic Fields whose Class Number is Unity." Bull. Amer. Math. Soc. 39, 360, 1933.

Montgomery, H. and Weinberger, P. "Notes on Small Class Numbers." Acta. Arith. 24, 529-542, 1974.

Oesterlé, J. "Nombres de classes des corps quadratiques imaginaires." Astérique 121-122, 309-323, 1985.

Oesterlé, J. "Le problème de Gauss sur le nombre de classes." Enseign Math. 34, 43-67, 1988.

Serre, J.-P. 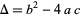." Math. Medley 13, 1-10, 1985.

Shanks, D. "On Gauss's Class Number Problems." Math. Comput. 23, 151-163, 1969.

Sloane, N. J. A. Sequence A003173/M0827 in "The On-Line Encyclopedia of Integer Sequences."

Stark, H. M. "A Complete Determination of the Complex Quadratic Fields of Class Number One." Michigan Math. J. 14, 1-27, 1967.

Stark, H. M. "On Complex Quadratic Fields with Class Number Two." Math. Comput. 29, 289-302, 1975.

Wagner, C. "Class Number 5, 6, and 7." Math. Comput. 65, 785-800, 1996.

Watkins, M. "Class Numbers of Imaginary Quadratic Fields." Math. Comput. 73, 907-938, 2004.

اخر الاخبار

اخبار العتبة العباسية المقدسة

أهالي كربلاء يحيون اليوم السابع لذكرى شهادة الإمام الحسين (عليه السلام)

مشروع أمير القراء الوطني يشهد مشاركة أكثر من 100 طالبٍ في مرحلته الثالثة

قسم الشؤون الفكرية يصدر دليلًا يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة

قسم الشؤون الفكرية يعلن عن توفير عددٍ من المكتبات الإلكترونية المتخصّصة للمؤسّسات الدينية والمكتبات العامّة

المزيد

الآخبار الصحية

نصائح عملية للحد من التعرق المفرط في الصيف

أطباء يحذرون: مكمل غذائي شائع قد يدمر الجهاز العصبي

تحذير طبي من تأثير جانبي "غير متوقع" لحقن التخسيس

حمامات الثلج قد تكون خطيرة وأحيانا مميتة.. ما السبب؟

المزيد

الآخبار التكنلوجية

أكبر جدارية شمسية في العالم تدخل موسوعة غينيس.. مشروع ضخم

تسارع دوران الأرض يثير القلق.. وتحذيرات من "كوارث محتملة" ؟

"سوذبيز" تطرح أكبر قطعة من المريخ على الأرض في مزاد علني

أوبن أيه آي تعتزم إطلاق متصفح إنترنت يعمل بالذكاء الاصطناعي

المزيد