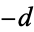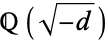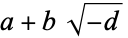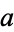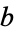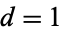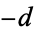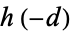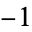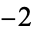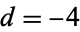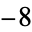The values of  for which imaginary quadratic fields  are uniquely factorable into factors of the form . Here,  and  are half-integers, except for  and 2, in which case they are integers. The Heegner numbers therefore correspond to binary quadratic form discriminants  which have class number  equal to 1, except for Heegner numbers  and , which correspond to  and , respectively.

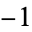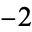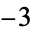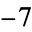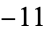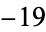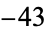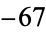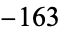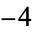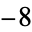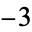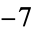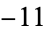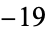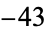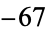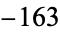The determination of these numbers is called Gauss's class number problem, and it is now known that there are only nine Heegner numbers: , , , , , , , , and  (OEIS A003173), corresponding to discriminants , , , , , , , , and , respectively. This was proved by Heegner (1952)--although his proof was not accepted as complete at the time (Meyer 1970)--and subsequently established by Stark (1967).

Heilbronn and Linfoot (1934) showed that if a larger 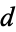 existed, it must be 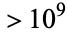. Heegner (1952) published a proof that only nine such numbers exist, but his proof was not accepted as complete at the time. Subsequent examination of Heegner's proof show it to be "essentially" correct (Conway and Guy 1996).

The Heegner numbers have a number of fascinating connections with amazing results in prime number theory. In particular, the j-function provides stunning connections between 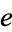, , 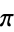and the algebraic integers. They also explain why Euler's prime-generating polynomial  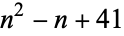is so surprisingly good at producing primes.

REFERENCES:

Conway, J. H. and Guy, R. K. "The Nine Magic Discriminants." In The Book of Numbers. New York: Springer-Verlag, pp. 224-226, 1996.

Heegner, K. "Diophantische Analysis und Modulfunktionen." Math. Z. 56, 227-253, 1952.

Heilbronn, H. A. and Linfoot, E. H. "On the Imaginary Quadratic Corpora of Class-Number One." Quart. J. Math. (Oxford) 5, 293-301, 1934.

Meyer, C. "Bemerkungen zum Satz von Heegner-Stark über die imaginär-quadratischen Zahlkörper mit der Klassenzahl Eins." J. reine angew. Math. 242, 179-214, 1970.

Sloane, N. J. A. Sequence A003173/M0827 in "The On-Line Encyclopedia of Integer Sequences."

Stark, H. M. "A Complete Determination of the Complex Quadratic Fields of Class Number One." Michigan Math. J. 14, 1-27, 1967.a

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الدينية يوزع أكثر من ألفي وجبة طعام للمعزين في ذكرى عاشوراء بنينوى

قسم الشؤون الطبية يواصل تقديم خدماته الصحية لزائري عاشوراء

جموع المعزين تحيي مراسم يوم العاشر من شهر المحرم عند المرقدين الطاهرين

قسم العلاقات يطلق محطات فتية الكفيل الثقافية في محافظة نينوى

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد