Chinese Hypothesis

The hypothesis that an integer 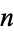 is prime iff it satisfies the condition that  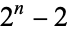is divisible by . Dickson (2005, p. 91) stated that Leibniz believe to have proved that this congruence implies that  is prime. In actuality, this condition is necessary but not sufficient for 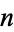 to be prime since, for example,  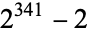is divisible by 341, but  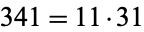is composite.

Composite numbers 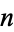 (such as 341) for which  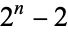is divisible by  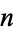are called Poulet numbers, and are a special class of Fermat pseudoprimes. The Chinese hypothesis is a special case of Fermat's little theorem.

The "Chinese hypothesis," "Chinese congruence," or "Chinese theorem," as it is sometimes called, is commonly attributed to Chinese scholars more than 2500 years ago. However, this oft-quoted attribution (e.g., Honsberger 1973, p. 3) is a myth originating with Jeans (1897-98), who wrote that "a paper found among those of the late Sir Thomas Wade and dating from the time of Confucius" contained the theorem. This assertion was refuted by Needham, who attributes the misunderstanding to an incorrect translation of a passage in a well-known book The Nine Chapters of Mathematical Art (Ribenboim 1996, p. 104). Qi (1991) attributed the hypothesis to Chinese mathematician Li Shan-Lan (1811-1882), communicated the statement to his collaborator in the translation of Western texts, and the collaborator then published it. Li subsequently learned that the statement was wrong, and hence did not publish it himself, but Hua Heng-Fang published the statement as if it were correct in 1882 (Ribenboim 1996, pp. 104-105).

REFERENCES:

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, 2005.

Erdős, P. "On the Converse of Fermat's Theorem." Amer. Math. Monthly 56, 623-624, 1949.

Honsberger, R. "An Old Chinese Theorem and Pierre de Fermat." Ch. 1 in Mathematical Gems I. Washington, DC: Math. Assoc. Amer., pp. 1-9, 1973.

Jeans, J. H. Messenger Math. 27, 1897-98.

Needham, J. (Ed.). Ch. 19 in Science and Civilisation in China, Vol. 3: Mathematics and the Sciences of the Heavens and the Earth. Cambridge, England: Cambridge University Press, 1959.

Qi, H. Transmission of Western Mathematics during the Kangxi Kingdom and Its Influence Over Chinese Mathematics. Ph.D. thesis. Beijing, 1991.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 103-105, 1996.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 19-20, 1993.

Yan, L. and Shiran, D. Chinese Mathematics, A Concise History. Oxford, England: Clarendon Press, 1987.