If 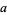 is an arbitrary integer relatively prime to  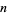and 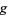 is a primitive root of 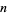, then there exists among the numbers 0, 1, 2, ..., 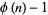, where  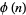is the totient function, exactly one number  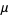such that

The number 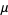 is then called the discrete logarithm of  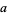with respect to the base  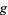modulo  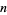and is denoted

The term "discrete logarithm" is most commonly used in cryptography, although the term "generalized multiplicative order" is sometimes used as well (Schneier 1996, p. 501). In number theory, the term "index" is generally used instead (Gauss 1801; Nagell 1951, p. 112).

For example, the number 7 is a positive primitive root of 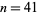 (in fact, the set of primitive roots of 41 is given by 6, 7, 11, 12, 13, 15, 17, 19, 22, 24, 26, 28, 29, 30, 34, 35), and since 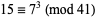, the number 15 has multiplicative order 3 with respect to base 7 (modulo 41) (Nagell 1951, p. 112). The generalized multiplicative order is implemented in the Wolfram Language as MultiplicativeOrder[g, n, {" src="http://mathworld.wolfram.com/images/equations/DiscreteLogarithm/Inline14.gif" style="height:15px; width:5px" />a1}" src="http://mathworld.wolfram.com/images/equations/DiscreteLogarithm/Inline15.gif" style="height:15px; width:5px" />], or more generally as MultiplicativeOrder[g, n, {" src="http://mathworld.wolfram.com/images/equations/DiscreteLogarithm/Inline16.gif" style="height:15px; width:5px" />a1, a2, ...}" src="http://mathworld.wolfram.com/images/equations/DiscreteLogarithm/Inline17.gif" style="height:15px; width:5px" />].

Discrete logarithms were mentioned by Charlie the math genius in the Season 2 episode "In Plain Sight" of the television crime drama NUMB3RS.

REFERENCES:

Gauss, C. F. §57 in Disquisitiones Arithmeticae. Leipzig, Germany, 1801. Reprinted New Haven, CT: Yale University Press, 1965.

Nagell, T. "Exponent of an Integer Modulo 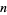" and "The Index Calculus." §31 and 33 in Introduction to Number Theory. New York: Wiley, pp. 102-106 and 111-115, 1951.

Schneier, B Applied Cryptography: Protocols, Algorithms, and Source Code in C, 2nd ed. New York: Wiley, 1996.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد