


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-2-2020
Date: 6-7-2020
Date: 15-12-2020
|
The Fermat quotient for a number 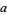 and a prime base
and a prime base 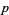 is defined as
is defined as
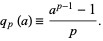 |
(1) |
If 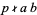 , then
, then
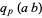 |
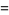 |
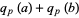 |
(2) |
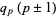 |
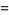 |
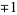 |
(3) |
(mod 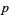 ), where the modulus is taken as a fractional congruence.
), where the modulus is taken as a fractional congruence.
The special case 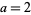 is given by
is given by
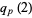 |
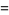 |
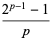 |
(4) |
 |
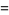 |
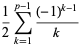 |
(5) |
 |
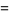 |
![1/2ln2+1/4(-1)^p[gamma_0(1/2(p+1))-gamma_0(1/2p)]](http://mathworld.wolfram.com/images/equations/FermatQuotient/Inline20.gif) |
(6) |
 |
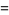 |
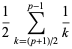 |
(7) |
 |
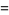 |
![1/2[gamma_0(p)-gamma_0(1/2(p+1))],](http://mathworld.wolfram.com/images/equations/FermatQuotient/Inline26.gif) |
(8) |
all again (mod 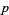 ) where the modulus is taken as a fractional congruence,
) where the modulus is taken as a fractional congruence, 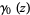 is the digamma function, and the last two equations hold for odd primes only.
is the digamma function, and the last two equations hold for odd primes only.
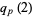 is an integer for
is an integer for 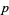 a prime, with the values for
a prime, with the values for 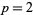 , 3, 5, ... being 1, 3, 2, 5, 3, 13, 3, 17, 1, 6, ....
, 3, 5, ... being 1, 3, 2, 5, 3, 13, 3, 17, 1, 6, ....
The quantity 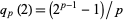 is known to be congruent to zero (mod
is known to be congruent to zero (mod 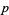 ) for only two primes: the so-called Wieferich primes 1093 and 3511 (Lehmer 1981, Crandall 1986).
) for only two primes: the so-called Wieferich primes 1093 and 3511 (Lehmer 1981, Crandall 1986).
REFERENCES:
Crandall, R. Projects in Scientific Computation. New York: Springer-Verlag, 1986.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 105, 2005.
Lehmer, D. H. "On Fermat's Quotient, Base Two." Math. Comput. 36, 289-290, 1981.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 70, 1986.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|