An unsolved problem in mathematics attributed to Lehmer (1933) that concerns the minimum Mahler measure 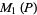 for a univariate polynomial  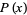that is not a product of cyclotomic polynomials. Lehmer (1933) conjectured that if  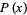is such an integer polynomial, then

			(1)
			(2)

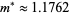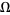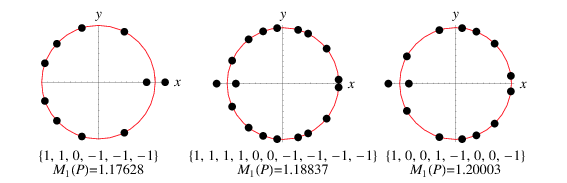
where , denoted  by Lehmer (1933) and 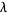 by Hironaka (2009), is the largest positive root of this polynomial. The roots of this polynomial, plotted in the left figure above, are very special, since 8 of the 10 lie on the unit circle in the complex plane. The roots of the polynomials (represented by half their coefficients) giving the two next smallest known Mahler measures are also illustrated above (Mossinghoff 1998, p. S11).

The best current bound is that of Smyth (1971), who showed that 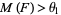, where  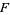is a nonzero nonreciprocal polynomial that is not a product of cyclotomic polynomials (Everest 1999), and  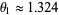is the real root of 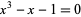. Generalizations of Smyth's result have been constructed by Lloyd-Smith (1985) and Dubickas (1997).

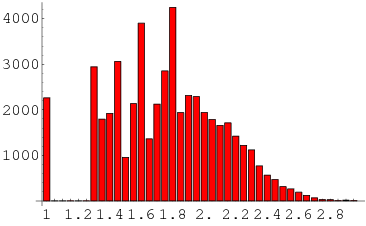
In general, the smallest Mahler measures occur for integer polynomials that are small in absolute value. The histogram above shows the distribution of measures for random 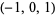-polynomials of random orders 1 to 10. Mossinghoff (1998) gives a table of the smallest known Mahler measures for polynomial degrees up to 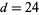, and subsequently demonstrated that  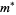is the smallest Mahler measure greater than 1 for all degrees up to 40 (Mossinghoff, Hironaka 2009).

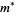 is a Salem constant.

REFERENCES:

Bailey, D. H. and Broadhurst, D. J. "A Seventeenth-Order Polylogarithm Ladder." 20 Jun 1999. http://arxiv.org/abs/math.CA/9906134.

Boyd, D. W. "Reciprocal Polynomials Having Small Measure." Math. Comput. 35, 1361-1377, 1980.

Boyd, D. W. "Reciprocal Polynomials Having Small Measure. II." Math. Comput. 53, 355-357 and S1-S5, 1989.

Dubickas, A. "Algebraic Conjugates Outside the Unit Circle." In New Trends in Probability and Statistics, Vol. 4: Analytic and Probabilistic Methods in Number Theory. Proceedings of the 2nd International Conference held in Honor of J. Kubilius on His 75th Birthday in Palanga, September 23-27, 1996 (Ed. A. Laurinčikas, E. Manstavičius, and V. Stakenas). Utrecht, Netherlands: VSP, pp. 11-21, 1997.

Everest, G. and Ward, T. Ch. 1 in Heights of Polynomials and Entropy in Algebraic Dynamics. London: Springer-Verlag, 1999.

Hironaka, E. "What Is... Lehmer's Number." Not. Amer. Math. Soc. 56, 374-375, 2009.

Lehmer, D. H. "Factorization of Certain Cyclotomic Functions." Ann. Math. 34, 461-469, 1933.

Lloyd-Smith, C. W. "Algebraic Numbers Near the Unit Circle." Acta Arith. 45, 43-57, 1985.

Mossinghoff, M. "Lehmer's Problem." http://oldweb.cecm.sfu.ca/~mjm/Lehmer/.

Mossinghoff, M. J. "Polynomials with Small Mahler Measure." Math. Comput. 67, 1697-1705 and S11-S14, 1998.

Smyth, C. J. "On the Product of the Conjugates Outside the Unit Circle of an Algebraic Integer." Bull. London Math. Soc. 3, 169-175, 1971.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد