Catalan,s Constant Digits
المؤلف:
Glaisher, J. W. L.
المصدر:
"On a Numerical Continued Product." Messenger Math. 6
الجزء والصفحة:
...
26-1-2020
1097
Catalan's Constant Digits
Based on methods developer in collaboration with M. Leclert, Catalan (1865) computed the constant
(OEIS A006752) now known as Catalans' constant to 9 decimals. In 1867, M. Bresse subsequently computed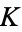 
to 24 decimal places using a technique from Kummer. Glaisher evaluated 
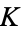to 20 (Glaisher 1877) and subsequently 32 decimal digits (Glaisher 1913). Catalan's constant was computed to 
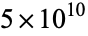decimal digits by A. Roberts on Dec. 13, 2010 (Yee).
The Earls sequence (starting position of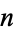 
copies of the digit 
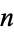) for Catalan's constant is given for 
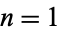, 2, ... by 2, 107, 1225, 596, 32187, 185043, 20444527, 92589355, 3487283621, ... (OEIS A224819).
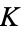-constant primes occur for 52, 276, 25477, ... (OEIS A118328) digits.
It is not known if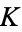 
is normal, but the following table giving the counts of digits in the first 
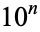terms shows that the decimal digits are very uniformly distributed up to at least 
.
 |
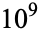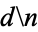OEIS |
10 |
100 |
 |
 |
 |
 |
 |
 |
 |
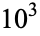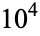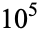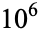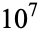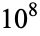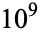| 0 |
A224615 |
0 |
6 |
98 |
976 |
9828 |
99620 |
999784 |
9998686 |
99996067 |
| 1 |
A224616 |
2 |
18 |
94 |
1039 |
9832 |
99697 |
1000293 |
10003813 |
100006305 |
| 2 |
A224696 |
0 |
10 |
93 |
980 |
10078 |
100168 |
1001789 |
10005122 |
100000806 |
| 3 |
A224706 |
0 |
7 |
104 |
1014 |
9859 |
99580 |
999672 |
9995676 |
100001483 |
| 4 |
A224717 |
1 |
11 |
107 |
961 |
10051 |
100074 |
1000165 |
9995377 |
100001871 |
| 5 |
A224774 |
3 |
10 |
89 |
1003 |
10062 |
100053 |
999965 |
9999309 |
100000777 |
| 6 |
A224775 |
1 |
12 |
78 |
985 |
9986 |
100201 |
998712 |
10000674 |
99998816 |
| 7 |
A224816 |
0 |
11 |
124 |
1032 |
10028 |
100083 |
1000510 |
10003863 |
100000576 |
| 8 |
A224817 |
0 |
3 |
102 |
1058 |
10192 |
100352 |
999298 |
9997437 |
100000863 |
| 9 |
A224818 |
3 |
12 |
111 |
952 |
10084 |
100172 |
999812 |
10000043 |
99992436 |
The digits 0123456789 do not occur in the first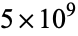 
decimal digits of 
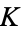, but 9876543210 does (once), starting at position 2748123761 (E. Weisstein, Aug. 7, 2013).
REFERENCES:
Glaisher, J. W. L. "On a Numerical Continued Product." Messenger Math. 6, 71-76, 1877.
Glaisher, J. W. L. "Numerical Values of the Series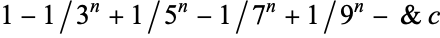 
for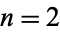 
, 4, 6." Messenger Math. 42, 35-58, 1913.
Sloane, N. J. A. Sequences A118328 and A224819 in "The On-Line Encyclopedia of Integer Sequences."
Yee, A. J. "y-cruncher - A Multi-Threaded Pi-Program." http://www.numberworld.org/y-cruncher/.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
