

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Euler Product
المؤلف:
Derbyshire, J.
المصدر:
Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
الجزء والصفحة:
...
4-2-2020
1665
Euler Product
For 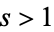 , the Riemann zeta function is given by
, the Riemann zeta function is given by
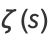 |
 |
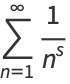 |
(1) |
 |
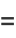 |
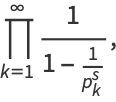 |
(2) |
where 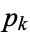 is the
is the 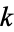 th prime. This is Euler's product (Whittaker and Watson 1990), called by Havil (2003, p. 61) the "all-important formula" and by Derbyshire (2004, pp. 104-106) the "golden key."
th prime. This is Euler's product (Whittaker and Watson 1990), called by Havil (2003, p. 61) the "all-important formula" and by Derbyshire (2004, pp. 104-106) the "golden key."
This can be proved by expanding the product, writing each term as a geometric series, expanding, multiplying, and rearranging terms,
![product_(k=1)^infty1/(1-1/(p_k^s))=1/(1-1/(p_1^s))1/(1-1/(p_2^s))1/(1-1/(p_3^s))...
=[sum_(k=0)^infty(1/(p_1^s))^k][sum_(k=0)^infty(1/(p_2^s))^k][sum_(k=0)^infty(1/(p_3^s))^k]...
=(1+1/(p_1^s)+1/(p_1^(2s))+1/(p_1^(3s))+...)(1+1/(p_2^s)+1/(p_2^(2s))+1/(p_2^(3s))+...)...
=1+sum_(1<=i)1/(p_i^s)+sum_(1<=i<=j)1/(p_i^sp_j^s)+sum_(1<=i<=j<=k)1/(p_i^sp_j^sp_k^s)+...
=1+1/(2^s)+1/(3^s)+1/(4^s)+1/(5^s)+...
=sum_(n=1)^infty1/(n^s)
=zeta(s).](http://mathworld.wolfram.com/images/equations/EulerProduct/NumberedEquation1.gif) |
(3) |
Here, the rearrangement leading to equation (1) follows from the fundamental theorem of arithmetic, since each product of prime powers appears in exactly one denominator and each positive integer equals exactly one product of prime powers.
This product is related to the Möbius function 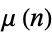 via
via
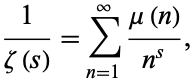 |
(4) |
which can be seen by expanding the product to obtain
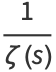 |
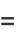 |
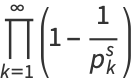 |
(5) |
 |
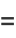 |
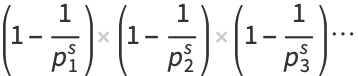 |
(6) |
 |
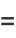 |
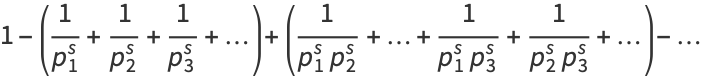 |
(7) |
 |
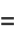 |
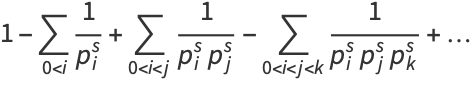 |
(8) |
 |
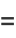 |
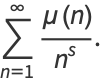 |
(9) |
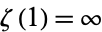 , but the finite product exists, giving
, but the finite product exists, giving
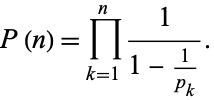 |
(10) |
For upper limits 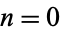 , 1, 2, ..., the products are given by 1, 2, 3, 15/4, 35/8, 77/16, 1001/192, 17017/3072, ... (OEIS A060753 and A038110). Premultiplying by
, 1, 2, ..., the products are given by 1, 2, 3, 15/4, 35/8, 77/16, 1001/192, 17017/3072, ... (OEIS A060753 and A038110). Premultiplying by 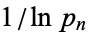 and letting
and letting 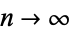 gives a beautiful result known as the Mertens theorem.
gives a beautiful result known as the Mertens theorem.
The Euler product appears briefly in a pan of John Nash's (played by Russell Crowe) blackboard scribblings in Ron Howard's 2001 film A Beautiful Mind.
REFERENCES:
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Edwards, H. M. "The Euler Product Formula." §1.2 in Riemann's Zeta Function. New York: Dover, pp. 6-7, 2001.
Euler, L. "Variae observationes circa series infinitas." St. Petersburg Acad., 1737.
Hardy, G. H. and Wright, E. M. "The Zeta Function." §17.2 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 245-247, 1979.
Havil, J. "The All-Important Formula." §7.1 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 61-62, 2003.
Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, p. 216, 1996.
Shimura, G. Euler Products and Eisenstein Series. Providence, RI: Amer. Math. Soc., 1997.
Sloane, N. J. A. Sequences A038110 and A060753 in "The On-Line Encyclopedia of Integer Sequences."
Whittaker, E. T. and Watson, G. N. "Euler's Product for 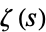 ." §13.3 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 271-272, 1990.
." §13.3 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 271-272, 1990.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















