
Triangle Triangle Picking
 المؤلف:
Sloane, N. J. A.
المؤلف:
Sloane, N. J. A.
 المصدر:
Sequences A103474, A103475, A130117, and A130118 in "The On-Line Encyclopedia of Integer Sequences."
المصدر:
Sequences A103474, A103475, A130117, and A130118 in "The On-Line Encyclopedia of Integer Sequences."
 الجزء والصفحة:
...
الجزء والصفحة:
...
 14-2-2020
14-2-2020
 1163
1163
Triangle Triangle Picking
The problem of finding the mean triangle area of a triangle with vertices picked inside a triangle with unit area was proposed by Watson (1865) and solved by Sylvester. It solution is a special case of the general formula for polygon triangle picking.
Since the problem is affine, it can be solved by considering for simplicity an isosceles right triangle with unit leg lengths. Integrating the formula for the area of a triangle over the six coordinates of the vertices (and normalizing to the area of the triangle and region of integration by dividing by the integral of unity over the region) gives
where
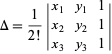 |
(3)
|
is the triangle area of a triangle with vertices 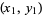 ,
, 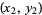 , and
, and 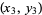 .
.
The integral can be solved using computer algebra by breaking up the integration region using cylindrical algebraic decomposition. This results in 62 regions, 30 of which have distinct integrals, each of which can be directly integrated. Combining the results then gives the result
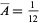 |
(4)
|
(Pfiefer 1989; Zinani 2003).
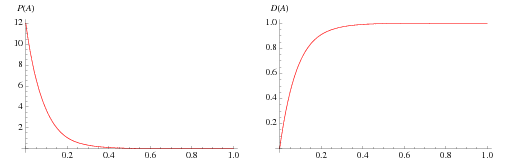
The exact distribution function  was derived by Philip.
was derived by Philip.  and
and 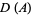 are given by
are given by
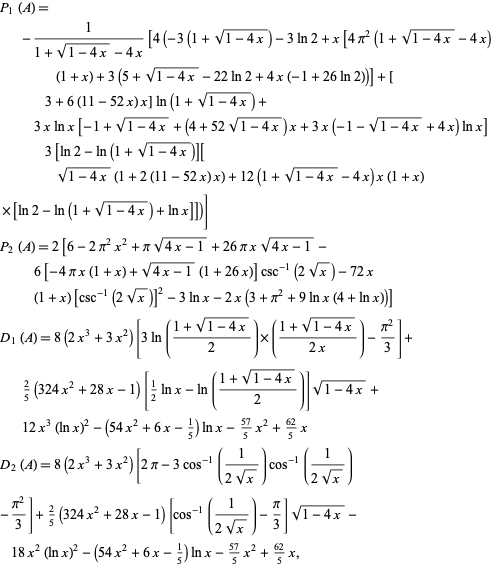 |
(5)
|
where the subscript 1 denotes the region with 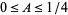 and 2 denotes the region with
and 2 denotes the region with 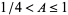 .
.
The raw moments 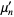 of
of 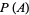 for
for 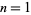 , 2, ... are 1/12, 1/144, 31/9000, 1/450, 1063/617400, 403/264600, ... (OEIS A103474 and A103475).
, 2, ... are 1/12, 1/144, 31/9000, 1/450, 1063/617400, 403/264600, ... (OEIS A103474 and A103475).
The central moments 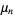 of
of 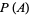 for
for 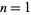 , 2, ... are 0, 1/144, 61/54000, 343/864000, 9493/66679200, ...
, 2, ... are 0, 1/144, 61/54000, 343/864000, 9493/66679200, ...
(OEIS A130117 and A130118).
REFERENCES:
Pfiefer, R. E. "The Historical Development of J. J. Sylvester's Four Point Problem." Math. Mag. 62, 309-317, 1989.
Philip, J. "The Area of a Random Convex Polygon in a Triangle." Tech. Report TRITA MAT 05 MA 04. n.d. http://www.math.kth.se/~johanph/area2.pdf.
Sloane, N. J. A. Sequences A103474, A103475, A130117, and A130118 in "The On-Line Encyclopedia of Integer Sequences."
Watson, S. "Question 1229." Mathematical Questions, with Their Solutions, from the Educational Times, Vol. 4. London: F. Hodgson and Son, p. 101, 1865.
Zinani, A. "The Expected Volume of a Tetrahedron Whose Vertices are Chosen at Random in the Interior of a Cube." Monatshefte Math. 139, 341-348, 2003.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


