


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-11-2020
Date: 27-8-2020
Date: 20-11-2019
|
The 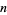 th Beraha constant (or number) is given by
th Beraha constant (or number) is given by
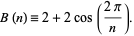 |
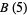 is
is 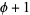 , where
, where 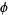 is the golden ratio,
is the golden ratio, 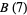 is the silver constant, and
is the silver constant, and 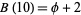 . The following table summarizes the first few Beraha numbers.
. The following table summarizes the first few Beraha numbers.
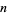 |
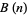 |
approx. |
| 1 | 4 | |
| 2 | 0 | |
| 3 | 1 | |
| 4 | 2 | |
| 5 | 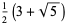 |
2.618 |
| 6 | 3 | |
| 7 | 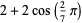 |
3.247 |
| 8 | 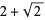 |
3.414 |
| 9 | 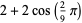 |
3.532 |
| 10 | 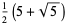 |
3.618 |
Noninteger Beraha numbers can never be roots of any chromatic polynomials with the possible exception of 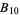 (G. Royle, pers. comm., Nov. 21, 2005). However, the roots of chromatic polynomials of planar triangulations appear to cluster around the Beraha numbers (and, technically, are conjectured to be accumulation points of roots of planar triangulation chromatic polynomials).
(G. Royle, pers. comm., Nov. 21, 2005). However, the roots of chromatic polynomials of planar triangulations appear to cluster around the Beraha numbers (and, technically, are conjectured to be accumulation points of roots of planar triangulation chromatic polynomials).
REFERENCES:
Beraha, S. Ph.D. thesis. Baltimore, MD: Johns Hopkins University, 1974.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 143, 1983.
Saaty, T. L. and Kainen, P. C. The Four-Color Problem: Assaults and Conquest. New York: Dover, pp. 160-163, 1986.
Tutte, W. T. "Chromials." University of Waterloo, 1971.
Tutte, W. T. "More about Chromatic Polynomials and the Golden Ratio." In Combinatorial Structures and their Applications: Proc. Calgary Internat. Conf., Calgary, Alberta, 1969. New York: Gordon and Breach, p. 439, 1969.
Tutte, W. T. "Chromatic Sums for Planar Triangulations I: The Case 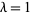 ." Research Report COPR 72-7, University of Waterloo, 1972a.
." Research Report COPR 72-7, University of Waterloo, 1972a.
Tutte, W. T. "Chromatic Sums for Planar Triangulations IV: The Case 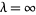 ." Research Report COPR 72-4, University of Waterloo, 1972b.
." Research Report COPR 72-4, University of Waterloo, 1972b.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|