


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-10-2020
Date: 28-8-2020
Date: 26-1-2021
|
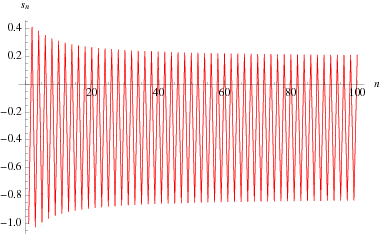
Consider the sequence of partial sums defined by
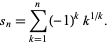 |
(1) |
As can be seen in the plot above, the sequence has two limit points at 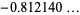 and 0.187859... (which are separated by exactly 1). The upper limit point is sometimes known as the MRB constant after the initials of its original investigator (Burns 1999; Plouffe).
and 0.187859... (which are separated by exactly 1). The upper limit point is sometimes known as the MRB constant after the initials of its original investigator (Burns 1999; Plouffe).
Sums for the MRB constant are given by
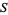 |
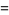 |
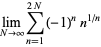 |
(2) |
 |
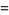 |
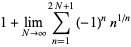 |
(3) |
 |
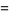 |
![sum_(k=1)^(infty)[(2k)^(1/(2k))-(2k-1)^(1/(2k-1))]](http://mathworld.wolfram.com/images/equations/MRBConstant/Inline10.gif) |
(4) |
 |
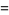 |
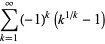 |
(5) |
 |
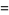 |
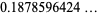 |
(6) |
(Finch 2003, p. 450; OEIS A037077).
The constant can also be given as a sum over derivatives of the Dirichlet eta function 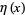 as
as
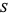 |
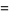 |
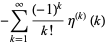 |
(7) |
 |
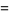 |
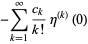 |
(8) |
where
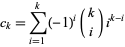 |
(9) |
and 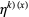 denotes the
denotes the 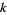 th derivative of
th derivative of 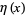 evaluated at
evaluated at  (Crandall 2012ab).
(Crandall 2012ab).
An integral expression for the constant is given by
![S=int_0^inftycsch(pit)I[(1+it)^(1/(1+it))]dt](http://mathworld.wolfram.com/images/equations/MRBConstant/NumberedEquation3.gif) |
(10) |
(M. Burns, pers. comm., Jan. 21, 2020).
No closed-form expression is known for this constant (Finch 2003, p. 450).
REFERENCES:
Burns, M. R. "An Alternating Series Involving 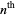 Roots." Unpublished note, 1999.
Roots." Unpublished note, 1999.
Burns, M. R. "Try to Beat These MRB Constant Records!" http://community.wolfram.com/groups/-/m/t/366628.
Crandall, R. E. "Unified Algorithms for Polylogarithm, 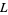 -Series, and Zeta Variants." 2012a. http://www.marvinrayburns.com/UniversalTOC25.pdf.
-Series, and Zeta Variants." 2012a. http://www.marvinrayburns.com/UniversalTOC25.pdf.
Crandall, R. E. "The MRB Constant." §7.5 in Algorithmic Reflections: Selected Works. PSI Press, pp. 28-29, 2012b.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 450, 2003.
Plouffe, S. "MRB Constant." http://pi.lacim.uqam.ca/piDATA/mrburns.txt.
Sloane, N. J. A. Sequences A037077 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|