Graham-Pollak Sequence
المؤلف:
Borwein, J. and Bailey, D
المصدر:
Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
الجزء والصفحة:
...
27-10-2020
2824
Graham-Pollak Sequence
Consider the recurrence equation defined by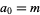 
and
 |
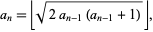(1)
|
where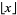 
is the floor function. Graham and Pollak actually defined 
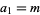, but the indexing 
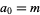will be used here for convenience, following Borwein and Bailey (2003, p. 62). The first few terms are summarized in the following table for small values of 
.
 |
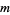OEIS |
 ,  , ... |
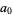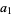| 1 |
A001521 |
1, 2, 3, 4, 6, 9, 13, 19, 27, 38, 54, ... |
| 5 |
A091522 |
5, 7, 10, 14, 20, 28, 40, 57, 81, 115, ... |
| 8 |
A091523 |
8, 12, 17, 24, 34, 48, 68, 96, 136, 193, ... |
Amazingly, an explicit formula for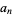 
with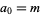 
is given by
 |
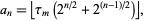(2)
|
where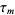 
is the 
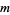th smallest number in the set ![<span style=]()
{1,2,3,...} union {sqrt(2),2sqrt(2),3sqrt(2),4sqrt(2),...}" src="https://mathworld.wolfram.com/images/equations/Graham-PollakSequence/Inline13.gif" style="height:22px; width:265px" /> (Graham and Pollak 1970; Borwein and Bailey 2003, p. 63).
Now consider the associated sequence
 |
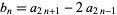(3)
|
whose value is always 0 or 1. Even more amazingly, interpreting the sequence ![<span style=]()
{b_k}" src="https://mathworld.wolfram.com/images/equations/Graham-PollakSequence/Inline14.gif" style="height:15px; width:23px" /> as a series of binary bits gives a series of algebraic constants
 |
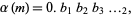(4)
|
where the first few constants are
(OEIS A091524 and A091525; Borwein and Bailey 2003, p. 63).
It is not known if sequences such as
 |
 |
 |
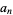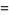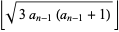(15)
|
 |
 |
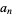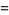![|_RadicalBox[<span style=]() {2, {a, _, {(, {n, -, 1}, )}}, {(, {{a, _, {(, {n, -, 1}, )}}, +, 1}, )}, {(, {{a, _, {(, {n, -, 1}, )}}, +, 2}, )}}, 3]_|" src="https://mathworld.wolfram.com/images/equations/Graham-PollakSequence/Inline50.gif" style="height:32px; width:176px" /> |
(16)
|
have corresponding properties (Graham and Pollak 1970; Borwein and Bailey 2003, p. 63).
REFERENCES:
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Ex. 3.46 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Graham, R. L. and Pollak, H. O. "Note of a Nonlinear Recurrence Related to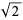 
." Math. Mag. 43, 143-145, 1970.
Guy, R. K. "The Strong Law of Small Numbers." Amer. Math. Monthly 95, 697-712, 1988.
Rabinowitz, S. and Gilbert, P. "A Nonlinear Recurrence Yielding Binary Digits." Math. Mag. 64, 168-171, 1991.
Sloane, N. J. A. Sequences A001521/M0569, A004539, A091522, A091523, A091524, and A091525 in "The On-Line Encyclopedia of Integer Sequences."
Stoll, T. "On Families of Nonlinear Recurrences Related to Digits." J. Integer Sequences 8, No. 05.3.2, 1-8, 2005. https://www.cs.uwaterloo.ca/journals/JIS/VOL8/Stoll/stoll56.pdf.
Stoll, T. "On a Problem of Erdős and Graham Concerning Digits." Acta Arith. 125, 89-100, 2006.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
