


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-11-2020
Date: 21-12-2020
Date: 5-11-2020
|
A fixed point is a point that does not change upon application of a map, system of differential equations, etc. In particular, a fixed point of a function 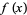 is a point
is a point 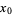 such that
such that
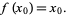 |
(1) |
The fixed point of a function 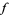 starting from an initial value
starting from an initial value  can be computed in the Wolfram Language using FixedPoint[f, x]. Similarly, to get a list of the values obtained by iterating the function until a fixed point is reached, the command FixedPointList[f, x] can be used.
can be computed in the Wolfram Language using FixedPoint[f, x]. Similarly, to get a list of the values obtained by iterating the function until a fixed point is reached, the command FixedPointList[f, x] can be used.
The following table lists the smallest positive fixed points for several simple functions.
| function | fixed point | OEIS |
| cosecant | 1.1141571408 | A133866 |
| cosine | 0.7390851332 | A003957 |
| cotangent | 0.8603335890 | A069855 |
| hyperbolic cosecant | 0.9320200293 | A133867 |
| hyperbolic cosine | -- | -- |
| hyperbolic cotangent | 1.1996786402 | A085984 |
| hyperbolic secant | 0.7650099545 | A069814 |
| hyperbolic sine | 0 | -- |
| hyperbolic tangent | 0 | -- |
| inverse cosecant | 1.1141571408 | A133866 |
| inverse cosine | 0.7390851332 | A003957 |
| inverse cotangent | 0.8603335890 | A069855 |
| inverse hyperbolic cosecant | 0.9320200293 | A133867 |
| inverse hyperbolic cosine | -- | -- |
| inverse hyperbolic cotangent | 1.1996786402 | A085984 |
| inverse hyperbolic secant | 0.7650099545 | A069814 |
| inverse hyperbolic sine | 0 | -- |
| inverse hyperbolic tangent | 0 | -- |
| inverse secant | -- | -- |
| inverse sine | 0 | -- |
| inverse tangent | 0 | -- |
| secant | 4.9171859252 | A133868 |
| sine | 0 | -- |
| tangent | 4.4934094579 | A115365 |
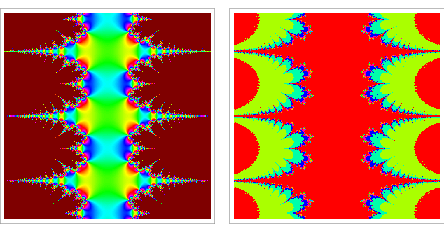
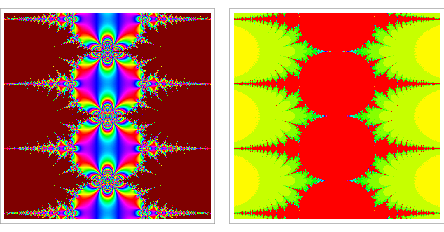
Fixed points of functions in the complex plane commonly lead to beautiful fractal structures. For example, the plots above color the value of the fixed point (left figures) and the number of iterations to reach a fixed point (right figures) for cosine (top) and sine (bottom). Newton's method, which essentially involves a fixed point computation in order to find roots, leads to similar fractals in an analogous way.
Points of an autonomous system of ordinary differential equations at which
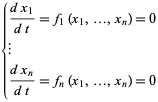 |
(2) |
are known as fixed points.
If a variable is slightly displaced from a fixed point, it may (1) move back to the fixed point ("asymptotically stable" or "superstable"), (2) move away ("unstable"), or (3) move in a neighborhood of the fixed point but not approach it ("stable" but not "asymptotically stable"). Fixed points are also called critical points or equilibrium points. If a variable starts at a point that is not a critical point, it cannot reach a critical point in a finite amount of time. Also, a trajectory passing through at least one point that is not a critical point cannot cross itself unless it is a closed curve, in which case it corresponds to a periodic solution.
A fixed point can be classified into one of several classes using linear stability analysis and the resulting stability matrix.
The following table summarizes types of possible fixed points for a two-dimensional system (Tabor 1989, pp. 22-24).
 |
fixed point |
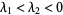 |
stable node |
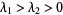 |
unstable node |
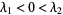 |
hyperbolic fixed point |
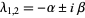 |
stable spiral point |
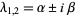 |
unstable spiral point |
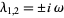 |
elliptic fixed point |
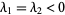 , ,  a null vector a null vector |
stable star |
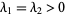 , , 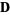 a null vector a null vector |
unstable star |
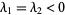 , , 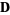 not a null vector not a null vector |
stable improper node |
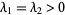 , , 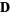 not a null vector not a null vector |
unstable improper node |
REFERENCES:
Shashkin, Yu. A. Fixed Points. Providence, RI: Amer. Math. Soc., 1991.
Tabor, M. "Linear Stability Analysis." §1.4 in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, pp. 20-31, 1989.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|