
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-2-2020
Date: 18-5-2020
Date: 18-5-2020
|
Van der Corput's constant is given by
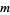 |
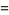 |
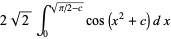 |
(1) |
 |
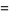 |
![2pi[coscC(phi)-sincS(phi)]](https://mathworld.wolfram.com/images/equations/vanderCorputsConstant/Inline6.gif) |
(2) |
 |
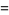 |
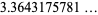 |
(3) |
(OEIS A143305), where 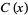 and
and 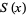 are Fresnel integrals,
are Fresnel integrals,
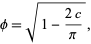 |
(4) |
and 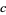 is the transcendental root of
is the transcendental root of
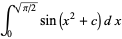 |
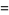 |
![2sqrt(pi)[coscC(phi)-sincS(phi)]](https://mathworld.wolfram.com/images/equations/vanderCorputsConstant/Inline15.gif) |
(5) |
 |
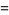 |
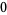 |
(6) |
with 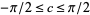 , namely
, namely
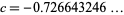 |
(7) |
(OEIS A143306).
REFERENCES:
Finch, S. R. "Van der Corput's Constant." §3.15 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 245-247, 2003.
Sloane, N. J. A. Sequences A143305 and A143306 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|