

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Khinchin,s Constant
المؤلف:
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E.
المصدر:
"On the Khintchine Constant." Math. Comput. 66
الجزء والصفحة:
...
4-5-2020
1298
Khinchin's Constant
Let
![x=[a_0;a_1,...]=a_0+1/(a_1+1/(a_2+1/(a_3+...)))](https://mathworld.wolfram.com/images/equations/KhinchinsConstant/NumberedEquation1.gif) |
(1) |
be the simple continued fraction of a "generic" real number  , where the numbers
, where the numbers 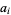 are the partial quotients. Khinchin (1934) considered the limit of the geometric mean
are the partial quotients. Khinchin (1934) considered the limit of the geometric mean
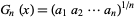 |
(2) |
as 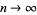 . Amazingly, except for a set of measure 0, this limit is a constant independent of
. Amazingly, except for a set of measure 0, this limit is a constant independent of  given by
given by
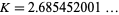 |
(3) |
(OEIS A002210), as proved in Kac (1959).
The constant is known as Khinchin's constant, and is commonly also spelled "Khintchine's constant" (Shanks and Wrench 1959, Bailey et al. 1997).
It is implemented as Khinchin, where its value is cached to 1100-digit precision. However, the numerical value of 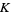 is notoriously difficult to calculate to high precision, so computation of more digits get increasingly slower.
is notoriously difficult to calculate to high precision, so computation of more digits get increasingly slower.
It is not known if 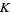 is irrational, let alone transcendental.
is irrational, let alone transcendental.
While it is known that almost all numbers  have limits
have limits 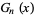 that approach
that approach 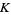 , this fact has not been proven for any explicit real number
, this fact has not been proven for any explicit real number  , e.g., a real number cast in terms of fundamental constants (Bailey et al. 1997).
, e.g., a real number cast in terms of fundamental constants (Bailey et al. 1997).
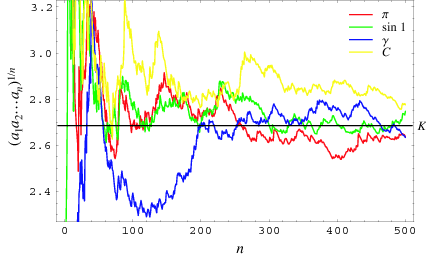
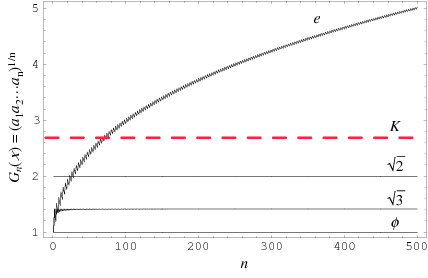
The values 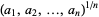 are plotted above for
are plotted above for 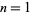 to 500 and
to 500 and 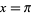 ,
, 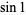 , the Euler-Mascheroni constant
, the Euler-Mascheroni constant 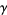 , and the Copeland-Erdős constant
, and the Copeland-Erdős constant 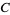 . Interestingly, the shape of the curves is almost identical to the corresponding curves for the Lévy constant.
. Interestingly, the shape of the curves is almost identical to the corresponding curves for the Lévy constant.
If 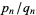 is the
is the 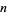 th convergent of the continued fraction of
th convergent of the continued fraction of  , then
, then
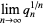 |
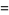 |
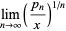 |
(4) |
 |
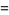 |
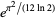 |
(5) |
 |
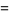 |
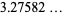 |
(6) |
(OEIS A086702) for almost all real  (Lévy 1936, Finch 2003), where
(Lévy 1936, Finch 2003), where 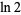 is the natural logarithm of 2. This number is sometimes called the Lévy constant.
is the natural logarithm of 2. This number is sometimes called the Lévy constant.
Product expressions for 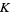 include
include
![K=product_(n=1)^infty[1+1/(n(n+2))]^(lnn/ln2)](https://mathworld.wolfram.com/images/equations/KhinchinsConstant/NumberedEquation4.gif) |
(7) |
(Shanks and Wrench 1959; Khinchin 1997, p. 93; Borwein and Bailey 2003, p. 25; Havil 2003, p. 161), where 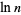 is the natural logarithm, and
is the natural logarithm, and
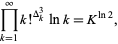 |
(8) |
where 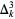 is the third-order finite difference operator, the latter of which obtained from three applications of summation by parts to the (logarithm of the) usual product definition (W. Gosper, pers. comm. Nov. 14, 2017).
is the third-order finite difference operator, the latter of which obtained from three applications of summation by parts to the (logarithm of the) usual product definition (W. Gosper, pers. comm. Nov. 14, 2017).
Products such as these can be converted to sums by taking the logarithm of both sides and using 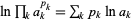 . Sums for
. Sums for 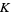 include
include
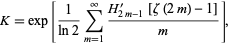 |
(9) |
where  is the Riemann zeta function and
is the Riemann zeta function and 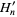 is an alternating harmonic number (Bailey et al. 1997),
is an alternating harmonic number (Bailey et al. 1997),
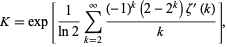 |
(10) |
where 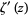 is the derivative of the Riemann zeta function (Gosper, pers. comm., Jun. 25, 1996) and the extremely rapidly converging sum originally due to Gosper (pers. comm., Jun. 25, 1996) and streamlined by O. Pavlyk (pers. comm., Apr. 24, 2006) is given by
is the derivative of the Riemann zeta function (Gosper, pers. comm., Jun. 25, 1996) and the extremely rapidly converging sum originally due to Gosper (pers. comm., Jun. 25, 1996) and streamlined by O. Pavlyk (pers. comm., Apr. 24, 2006) is given by
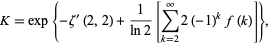 |
(11) |
where
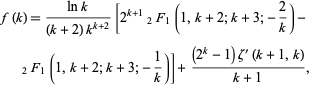 |
(12) |
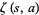 is a Hurwitz zeta function,
is a Hurwitz zeta function, 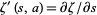 , and
, and 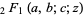 is a hypergeometric function.
is a hypergeometric function.
Khinchin's constant is also given by the integrals
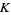 |
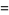 |
(13) |
|
 |
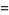 |
![2exp[1/(ln2)int_0^11/(x(1+x))ln[Gamma(2-x)Gamma(2+x)]dx]](https://mathworld.wolfram.com/images/equations/KhinchinsConstant/Inline47.gif) |
(14) |
(Shanks and Wrench 1959) and
![K=exp[(pi^2)/(12ln2)+1/2ln2+1/(ln2)int_0^pi(ln(theta|cottheta|)dtheta)/theta].](https://mathworld.wolfram.com/images/equations/KhinchinsConstant/NumberedEquation10.gif) |
(15) |
Corless (1992) showed that
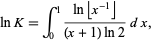 |
(16) |
with an analogous formula for the Lévy constant.
Real numbers  for which
for which 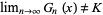 include
include 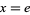 ,
, 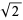 ,
, 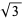 , and the golden ratio
, and the golden ratio 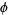 , plotted above.
, plotted above.
Amazingly, the constant 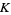 is simply the limiting case
is simply the limiting case 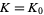 of a class of means defined by
of a class of means defined by
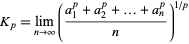 |
(17) |
for real 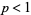 whose values are given by
whose values are given by
|
(18) |
(Ryll-Nardzewski 1951; Bailey et al. 1997; Khinchin 1997). An integral representation for 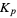 is given by
is given by
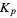 |
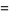 |
![[1/(ln2)int_0^1(|_1/t_|^p)/(t+1)dt]^(1/p)](https://mathworld.wolfram.com/images/equations/KhinchinsConstant/Inline60.gif) |
(19) |
 |
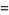 |
![[1/(ln2)sum_(k=1)^(infty)k^pln(1+1/(k(k+2)))]^(1/p)](https://mathworld.wolfram.com/images/equations/KhinchinsConstant/Inline63.gif) |
(20) |
for 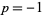 ,
, 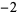 , ... (Iosifescu and Kraaikamp 2002, p. 231).
, ... (Iosifescu and Kraaikamp 2002, p. 231).
The constant
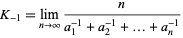 |
(21) |
is sometimes known as the Khinchin harmonic mean and is the 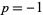 case of an infinite family of such constants of which
case of an infinite family of such constants of which 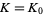 and
and 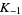 are the first two members.
are the first two members.
Define the following quantity in terms of the 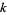 th partial quotient
th partial quotient 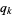 ,
,
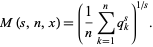 |
(22) |
Then
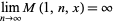 |
(23) |
for almost all real  (Khintchine 1934, 1936, Knuth 1981, Finch 2003), and
(Khintchine 1934, 1936, Knuth 1981, Finch 2003), and
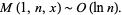 |
(24) |
Furthermore, for 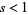 , the limiting value
, the limiting value
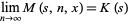 |
(25) |
exists and is a constant 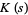 with probability 1 (Rockett and Szüsz 1992, Khinchin 1997).
with probability 1 (Rockett and Szüsz 1992, Khinchin 1997).
REFERENCES:
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E. "On the Khintchine Constant." Math. Comput. 66, 417-431, 1997.
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Corless, R. M. "Continued Fractions and Chaos." Amer. Math. Monthly 99, 203-215, 1992.
Finch, S. R. "Khintchine-Lévy Constants." §1.8 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 59-65, 2003.
Gosper, R. W. "Simpler Khinchine [was: Re: my two cents]" math-fun@cs.arizona.edu mailing list. 25 Jun 1996.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 159, 2003.
Iosifescu, M. and Kraaikamp, C. Metrical Theory of Continued Fractions. Amsterdam, Netherlands: Kluwer, 2002.
Kac, M. Statistical Independence in Probability, Analysis and Number Theory. Providence, RI: Math. Assoc. Amer., 1959.
Khinchin, A. Ya. "Average Values." §16 in Continued Fractions. New York: Dover, pp. 86-94, 1997.
Khintchine, A. "Metrische Kettenbruchprobleme." Compositio Math. 1, 361-382, 1934.
Khintchine, A. "Metrische Kettenbruchprobleme." Compositio Math. 2, 276-285, 1936.
Knuth, D. E. Exercise 24 in The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, p. 604, 1998.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1983.
Lehmer, D. H. "Note on an Absolute Constant of Khintchine." Amer. Math. Monthly 46, 148-152, 1939.
Lévy, P. "Sur les lois de probabilité dont dependent les quotients complets et incomplets d'une fraction continue." Bull. Soc. Math. France 57, 178-194, 1929.
Lévy, P. "Sur le développement en fraction continue d'un nombre choisi au hasard." Compositio Math. 3, 286-303, 1936. Reprinted in Œuvres de Paul Lévy, Vol. 6. Paris: Gauthier-Villars, pp. 285-302, 1980.
Phillipp, W. "Some Metrical Theorems in Number Theory." Pacific J. Math. 20, 109-127, 1967.
Rockett, A. M. and Szüsz, P. Continued Fractions. Singapore: World Scientific, 1992.
Ryll-Nardzewski, C. "On the Ergodic Theorems (I,II)." Studia Math. 12, 65-79, 1951.
Shanks, D. "Note MTE 164." Math. Tables Aids Comput. 4, 28, 1950.
Shanks, D. and Wrench, J. W. Jr. "Khintchine's Constant." Amer. Math. Monthly 66, 148-152, 1959.
Sloane, N. J. A. Sequences A002210/M1564, A002211/M0118, A086702, A087491, A087492, A087493, A087494, A087495, A087496, A087497, A087498, A087499, and A087500 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. "Khinchin's Constant." §8.4 in Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 163-171, 1991.
Wrench, J. W. Jr. "Further Evaluation of Khinchin's Constant." Math. Comput. 14, 370-371, 1960.
Wrench, J. W. Jr. and Shanks, D. "Questions Concerning Khintchine's Constant and the Efficient Computation of Regular Continued Fractions." Math. Comput. 20, 444-448, 1966.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















