


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-2-2020
Date: 3-11-2019
Date: 1-9-2020
|
A noble number  is defined as an irrational number having a continued fraction that becomes an infinite sequence of 1s at some point,
is defined as an irrational number having a continued fraction that becomes an infinite sequence of 1s at some point,
![nu=[0,a_1,a_2,...,a_n,1^_].](https://mathworld.wolfram.com/images/equations/NobleNumber/NumberedEquation1.gif) |
The prototype is the inverse of the golden ratio 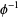 , whose continued fraction is composed entirely of 1s (except for the
, whose continued fraction is composed entirely of 1s (except for the 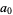 term),
term), ![[0,1^_]](https://mathworld.wolfram.com/images/equations/NobleNumber/Inline4.gif) .
.
Any noble number can be written as
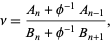 |
where 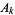 and
and 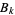 are the numerator and denominator of the
are the numerator and denominator of the 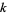 th convergent of
th convergent of ![[0,a_1,a_2,...,a_n]](https://mathworld.wolfram.com/images/equations/NobleNumber/Inline8.gif) .
.
The noble numbers are a subset of 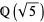 but not a subfield, since there is no subfield lying properly between
but not a subfield, since there is no subfield lying properly between 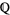 and
and 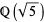 . To see this, consider
. To see this, consider 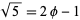 , which must be contained in the same field as
, which must be contained in the same field as 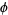 but is not a noble number since its continued fraction is
but is not a noble number since its continued fraction is ![[2,4^_]](https://mathworld.wolfram.com/images/equations/NobleNumber/Inline14.gif) .
.
REFERENCES:
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, p. 236, 1979.
Schroeder, M. "Noble and Near Noble Numbers." In Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, pp. 392-394, 1991.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|