


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-7-2020
Date: 2-5-2020
Date: 8-3-2020
|
Ramanujan developed a number of interesting closed-form expressions for generalized continued fractions. These include the almost integers
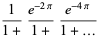 |
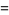 |
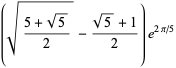 |
(1) |
 |
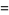 |
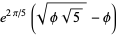 |
(2) |
 |
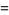 |
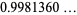 |
(3) |
(OEIS A091667; Watson 1929, 1931; Hardy 1999, p. 8), where 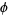 is the golden ratio, its multiplicative inverse
is the golden ratio, its multiplicative inverse
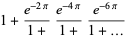 |
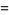 |
![1/2[1+sqrt(5)+sqrt(2(5+sqrt(5)))]e^(-2pi/5)](https://mathworld.wolfram.com/images/equations/RamanujanContinuedFractions/Inline13.gif) |
(4) |
 |
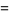 |
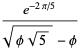 |
(5) |
 |
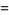 |
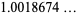 |
(6) |
(OEIS A091899; Ramanathan 1984), and
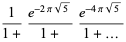 |
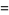 |
![{(sqrt(5))/(1+[5^(3/4)(phi-1)^(5/2)-1]^(1/5))-phi}e^(2pi/sqrt(5))](https://mathworld.wolfram.com/images/equations/RamanujanContinuedFractions/Inline22.gif) |
(7) |
 |
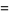 |
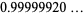 |
(8) |
(OEIS A091668; Watson 1929, 1931; Ramanathan 1984; Berndt and Rankin 1995, p. 57; Hardy 1999, p. 8) and its multiplicative inverse
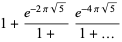 |
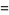 |
![(e^(-2pi/5))/((sqrt(5))/(1+[5^(3/4)(phi-1)^(5/2)]^(1/5))-phi)](https://mathworld.wolfram.com/images/equations/RamanujanContinuedFractions/Inline28.gif) |
(9) |
 |
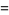 |
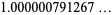 |
(10) |
(OEIS A091900).
Other examples include the integrals
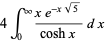 |
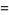 |
![1/2[zeta(2,1/4(1+sqrt(5)))-zeta(2,1/4(3+sqrt(5))]](https://mathworld.wolfram.com/images/equations/RamanujanContinuedFractions/Inline34.gif) |
(11) |
 |
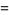 |
![1/2[psi_1(1/4(1+sqrt(5)))-psi_1(1/4(3+sqrt(5)))]](https://mathworld.wolfram.com/images/equations/RamanujanContinuedFractions/Inline37.gif) |
(12) |
 |
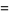 |
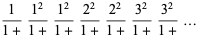 |
(13) |
 |
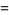 |
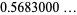 |
(14) |
(OEIS A091659; Preece 1931; Perron 1953; Berndt and Rankin 1995, pp. 57 and 65; Hardy 1999, p. 8), where 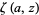 is the Hurwitz zeta function and
is the Hurwitz zeta function and 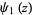 is the trigamma function, and
is the trigamma function, and
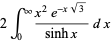 |
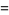 |
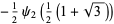 |
(15) |
 |
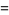 |
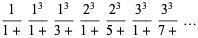 |
(16) |
 |
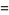 |
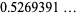 |
(17) |
(OEIS A091660; Preece 1931; Perron 1953; Berndt and Rankin 1995, pp. 57 and 65), where 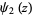 is a polygamma function.
is a polygamma function.
REFERENCES:
Berndt, B. C. and Rankin, R. A. Ramanujan: Letters and Commentary. Providence, RI: Amer. Math. Soc., 1995.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Perron, O. "Über die Preeceschen Kettenbrüche." Sitz. Bayer. Akad. Wiss. München Math. Phys. Kl., 21-56, 1953.
Preece, C. T. "Theorems Stated by Ramanujan (X)." J. London Math. Soc. 6, 22-32, 1931.
Ramanathan, K. G. "On Ramanujan's Continued Fraction." Acta. Arith. 43, 209-226, 1984.
Sloane, N. J. A. Sequences A091659, A091660, A091667, A091668, A091899, and A091900 in "The On-Line Encyclopedia of Integer Sequences."
Watson, G. N. "Theorems Stated by Ramanujan (VII): Theorems on a Continued Fraction." J. London Math. Soc. 4, 39-48, 1929.
Watson, G. N. "Theorems Stated by Ramanujan (IX): Two Continued Fractions." J. London Math. Soc. 4, 231-237, 1929.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|