


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-10-2019
Date: 14-7-2020
Date: 3-2-2020
|
A Diophantine equation is an equation in which only integer solutions are allowed.
Hilbert's 10th problem asked if an algorithm existed for determining whether an arbitrary Diophantine equation has a solution. Such an algorithm does exist for the solution of first-order Diophantine equations. However, the impossibility of obtaining a general solution was proven by Yuri Matiyasevich in 1970 (Matiyasevich 1970, Davis 1973, Davis and Hersh 1973, Davis 1982, Matiyasevich 1993) by showing that the relation 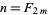 (where
(where 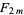 is the
is the 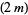 th Fibonacci number) is Diophantine. More specifically, Matiyasevich showed that there is a polynomial
th Fibonacci number) is Diophantine. More specifically, Matiyasevich showed that there is a polynomial 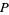 in
in 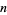 ,
, 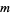 , and a number of other variables
, and a number of other variables  ,
, 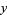 ,
, 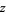 , ... having the property that
, ... having the property that 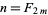 iff there exist integers
iff there exist integers  ,
, 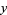 ,
, 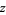 , ... such that
, ... such that 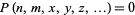 .
.
Matiyasevich's result filled a crucial gap in previous work by Martin Davis, Hilary Putnam, and Julia Robinson. Subsequent work by Matiyasevich and Robinson proved that even for equations in thirteen variables, no algorithm can exist to determine whether there is a solution. Matiyasevich then improved this result to equations in only nine variables (Jones and Matiyasevich 1982).
Ogilvy and Anderson (1988) give a number of Diophantine equations with known and unknown solutions.
A linear Diophantine equation (in two variables) is an equation of the general form
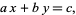 |
(1) |
where solutions are sought with 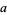 ,
, 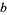 , and
, and 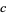 integers. Such equations can be solved completely, and the first known solution was constructed by Brahmagupta. Consider the equation
integers. Such equations can be solved completely, and the first known solution was constructed by Brahmagupta. Consider the equation
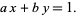 |
(2) |
Now use a variation of the Euclidean algorithm, letting 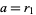 and
and 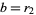
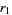 |
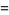 |
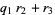 |
(3) |
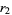 |
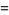 |
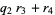 |
(4) |
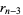 |
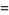 |
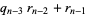 |
(5) |
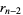 |
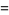 |
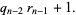 |
(6) |
Starting from the bottom gives
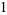 |
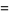 |
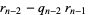 |
(7) |
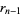 |
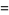 |
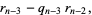 |
(8) |
so
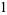 |
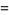 |
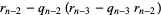 |
(9) |
 |
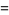 |
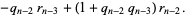 |
(10) |
Continue this procedure all the way back to the top.
Take as an example the equation
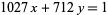 |
(11) |
and apply the algorithm above to obtain
 |
(12) |
The solution is therefore 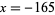 ,
, 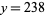 .
.
The above procedure can be simplified by noting that the two leftmost columns are offset by one entry and alternate signs, as they must since
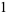 |
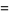 |
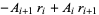 |
(13) |
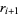 |
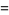 |
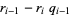 |
(14) |
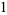 |
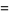 |
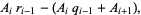 |
(15) |
so the coefficients of 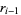 and
and 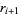 are the same and
are the same and
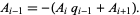 |
(16) |
Repeating the above example using this information therefore gives
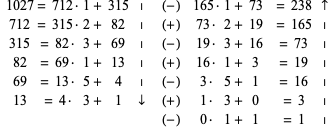 |
(17) |
and we recover the above solution.
Call the solutions to
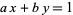 |
(18) |
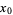 and
and 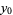 . If the signs in front of
. If the signs in front of 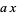 or
or 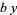 are negative, then solve the above equation and take the signs of the solutions from the following table:
are negative, then solve the above equation and take the signs of the solutions from the following table:
| equation |  |
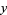 |
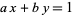 |
 |
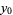 |
 |
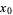 |
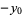 |
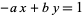 |
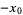 |
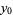 |
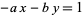 |
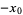 |
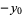 |
In fact, the solution to the equation
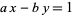 |
(19) |
is equivalent to finding the continued fraction for 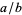 , with
, with 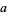 and
and 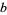 relatively prime (Olds 1963). If there are
relatively prime (Olds 1963). If there are 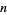 terms in the fraction, take the
terms in the fraction, take the 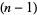 th convergent
th convergent 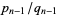 . But
. But
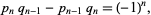 |
(20) |
so one solution is 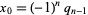 ,
, 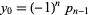 , with a general solution
, with a general solution
 |
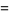 |
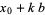 |
(21) |
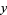 |
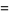 |
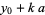 |
(22) |
with 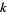 an arbitrary integer. The solution in terms of smallest positive integers is given by choosing an appropriate
an arbitrary integer. The solution in terms of smallest positive integers is given by choosing an appropriate 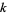 .
.
Now consider the general first-order equation of the form
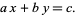 |
(23) |
The greatest common divisor 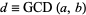 can be divided through yielding
can be divided through yielding
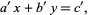 |
(24) |
where 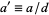 ,
, 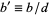 , and
, and 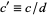 . If
. If 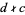 , then
, then 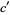 is not an integer and the equation cannot have a solution in integers. A necessary and sufficient condition for the general first-order equation to have solutions in integers is therefore that
is not an integer and the equation cannot have a solution in integers. A necessary and sufficient condition for the general first-order equation to have solutions in integers is therefore that 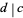 . If this is the case, then solve
. If this is the case, then solve
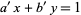 |
(25) |
and multiply the solutions by 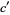 , since
, since
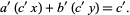 |
(26) |
D. Wilson has compiled a list of the smallest  th powers of positive integers that are the sums of the
th powers of positive integers that are the sums of the  th powers of distinct smaller positive integers. The first few are 3, 5, 6, 15, 12, 25, 40, ...(OEIS A030052):
th powers of distinct smaller positive integers. The first few are 3, 5, 6, 15, 12, 25, 40, ...(OEIS A030052):
 |
 |
 |
(27) |
 |
 |
 |
(28) |
 |
 |
 |
(29) |
 |
 |
 |
(30) |
 |
 |
 |
(31) |
 |
 |
 |
(32) |
 |
 |
 |
(33) |
 |
 |
 |
(34) |
 |
 |
 |
(35) |
 |
 |
 |
(36) |
REFERENCES:
Alpern, D. "Sums of Powers." https://www.alpertron.com.ar/SUMPOWER.HTM.
Bashmakova, I. G. Diophantus and Diophantine Equations. Washington, DC: Math. Assoc. Amer., 1997.
Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Carmichael, R. D. The Theory of Numbers, and Diophantine Analysis. New York: Dover, 1959.
Courant, R. and Robbins, H. "Continued Fractions. Diophantine Equations." §2.4 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 49-51, 1996.
Davis, M. "Hilbert's Tenth Problem is Unsolvable." Amer. Math. Monthly 80, 233-269, 1973.
Davis, M. and Hersh, R. "Hilbert's 10th Problem." Sci. Amer. 229, 84-91, Nov. 1973.
Davis, M. "Hilbert's Tenth Problem is Unsolvable." Appendix 2 in Computability and Unsolvability. New York: Dover, 1999-235, 1982.
Dickson, L. E. "Linear Diophantine Equations and Congruences." Ch. 2 in History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 41-99, 2005.
dmoz. "Equal Sums of Like Powers." https://dmoz.org/Science/Math/Number_Theory/Diophantine_Equations/Equal_Sums_of_Like_Powers/.
Dörrie, H. "The Fermat-Gauss Impossibility Theorem." §21 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 96-104, 1965.
Ekl, R. L. "New Results in Equal Sums of Like Powers." Math. Comput. 67, 1309-1315, 1998.
Guy, R. K. "Diophantine Equations." Ch. D in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 139-198, 1994.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Hunter, J. A. H. and Madachy, J. S. "Diophantos and All That." Ch. 6 in Mathematical Diversions. New York: Dover, pp. 52-64, 1975.
Ireland, K. and Rosen, M. "Diophantine Equations." Ch. 17 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 269-296, 1990.
Jones, J. P. and Matiyasevich, Yu. V. "Exponential Diophantine Representation of Recursively Enumerable Sets." Proceedings of the Herbrand Symposium, Marseilles, 1981. Amsterdam, Netherlands: North-Holland, pp. 159-177, 1982.
Lang, S. Introduction to Diophantine Approximations, 2nd ed. New York: Springer-Verlag, 1995.
Matiyasevich, Yu. V. "Solution of the Tenth Problem of Hilbert." Mat. Lapok 21, 83-87, 1970.
Matiyasevich, Yu. V. Hilbert's Tenth Problem. Cambridge, MA: MIT Press, 1993. https://www.informatik.uni-stuttgart.de/ifi/ti/personen/Matiyasevich/H10Pbook/.
Meyrignac, J.-C. "Computing Minimal Equal Sums of Like Powers." https://euler.free.fr/.
Mordell, L. J. Diophantine Equations. New York: Academic Press, 1969.
Nagell, T. "Diophantine Equations of First Degree." §10 in Introduction to Number Theory. New York: Wiley, pp. 29-32, 1951.
Ogilvy, C. S. and Anderson, J. T. "Diophantine Equations." Ch. 6 in Excursions in Number Theory. New York: Dover, pp. 65-83, 1988.
Olds, C. D. Ch. 2 in Continued Fractions. New York: Random House, 1963.
Sloane, N. J. A. Sequence A030052 in "The On-Line Encyclopedia of Integer Sequences."
Weisstein, E. W. "Books about Diophantine Equations." https://www.ericweisstein.com/encyclopedias/books/DiophantineEquations.html.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|