


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-1-2021
Date: 17-11-2020
Date: 29-12-2020
|
A Heronian tetrahedron, also called a perfect tetrahedron, is a (not necessarily regular) tetrahedron whose sides, face areas, and volume are all rational numbers. It therefore is a tetrahedron all of whose faces are Heronian triangles and additionally that has rational volume. (Note that the volume of a tetrahedron can be computed using the Cayley-Menger determinant.)
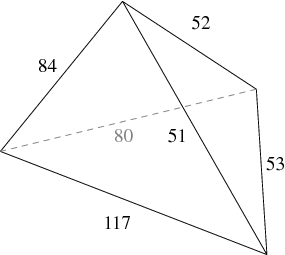
The integer Heronian tetrahedron having smallest maximum side length is the one with edge lengths 51, 52, 53, 80, 84, 117; faces (117, 80, 53), (117, 84, 51), (80, 84, 52), (53, 51, 52); face areas 1170, 1800, 1890, 2016; and volume 18144 (Buchholz 1992; Guy 1994, p. 191). This is the only integer Heronian triangle with all side lengths less than 157.
The integer Heronian tetrahedron with smallest possible surface area and volume has edges 25, 39, 56, 120, 153, and 160; areas 420, 1404, 1872, and 2688 (for a total surface area of 6384); and volume 8064 (Buchholz 1992, Peterson 2003).
R. Rathbun has cataloged Heronian triangles with perimeters smaller than 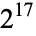 . This catalog allows the following special sets of Heronian tetrahedra to be identified. The following table gives the smallest pair of primitive integer Heronian tetrahedra with the same surface area.
. This catalog allows the following special sets of Heronian tetrahedra to be identified. The following table gives the smallest pair of primitive integer Heronian tetrahedra with the same surface area.
| area | volume | edges |
| 64584 | 170016 | 595, 429, 208, 116, 276, 325 |
| 64584 | 200928 | 595, 507, 116, 208, 276, 325 |
The following table gives the smallest pair of primitive integer Heronian tetrahedra with the same volume.
| area | volume | edges |
| 244272 | 3564288 | 697, 697, 306, 185, 185, 672 |
| 298248 | 3564288 | 1344, 697, 697, 153, 680, 680 |
Finally, the smallest triple of primitive integer Heronian tetrahedra with the same volume is given in the following table.
| area | volume | edges |
| 11124120 | 501399360 | 15080, 14820, 500, 1309, 1557, 13621 |
| 12571944 | 501399360 | 4522, 3485, 3485, 2640, 2275, 2275 |
| 12667452 | 501399360 | 5280, 3485, 3485, 2261, 2652, 2652 |
The smallest examples of integer Heronian tetrahedra composed of four identical copies of a single acute triangle (i.e., disphenoids) have pairs of opposite sides (148, 195, 203), (533, 875, 888), (1183, 1479, 1804), (2175, 2296, 2431), (1825, 2748, 2873), (2180, 2639, 3111), (1887, 5215, 5512), (6409, 6625, 8484), and (8619, 10136, 11275) (Guy 1994, p. 190; Buchholz 1992).
REFERENCES:
Buchholz, R. H. "Perfect Pyramids." Bull. Austral. Math. Soc. 45, 353-368, 1992.
Guy, R. K. "Simplexes with Rational Contents." §D22 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 190-192, 1994.
Peterson, I. "MathTrek: Euler Bricks and Perfect Polyhedra." Oct. 23, 1999. https://www.sciencenews.org/sn_arc99/10_23_99/mathland.htm.
Peterson, I. "MathTrek: Perfect Pyramids." July 26, 2003. https://www.sciencenews.org/20030726/mathtrek.asp.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|