
Mordell Curve
 المؤلف:
Apostol, T. M
المؤلف:
Apostol, T. M
 المصدر:
Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
المصدر:
Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 10-7-2020
10-7-2020
 1608
1608
Mordell Curve
An elliptic curve of the form  for
for  an integer. This equation has a finite number of solutions in integers for all nonzero
an integer. This equation has a finite number of solutions in integers for all nonzero  . If
. If  is a solution, it therefore follows that
is a solution, it therefore follows that  is as well.
is as well.
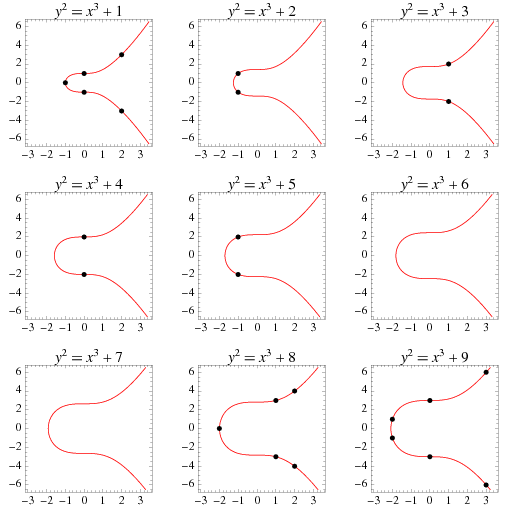
Uspensky and Heaslet (1939) give elementary solutions for  ,
,  , and 2, and then give
, and 2, and then give  ,
,  ,
,  , and 1 as exercises. Euler found that the only integer solutions to the particular case
, and 1 as exercises. Euler found that the only integer solutions to the particular case  (a special case of Catalan's conjecture) are
(a special case of Catalan's conjecture) are  ,
,  , and
, and  . This can be proved using Skolem's method, using the Thue equation
. This can be proved using Skolem's method, using the Thue equation  , using 2-descent to show that the elliptic curve has rank 0, and so on. It is given as exercise 6b in Uspensky and Heaslet (1939, p. 413), and proofs published by Wakulicz (1957), Mordell (1969, p. 126), Sierpiński and Schinzel (1988, pp. 75-80), and Metsaenkylae (2003).
, using 2-descent to show that the elliptic curve has rank 0, and so on. It is given as exercise 6b in Uspensky and Heaslet (1939, p. 413), and proofs published by Wakulicz (1957), Mordell (1969, p. 126), Sierpiński and Schinzel (1988, pp. 75-80), and Metsaenkylae (2003).
Solutions of the Mordell curve with  are summarized in the table below for small
are summarized in the table below for small  .
.
 |
solutions |
| 1 |
 |
| 2 |
 |
| 3 |
 |
| 4 |
 |
| 5 |
 |
| 6 |
none |
| 7 |
none |
| 8 |
 |
| 9 |
 |
| 10 |
 |
Values of  such that the Mordell curve has no integer solutions are given by 6, 7, 11, 13, 14, 20, 21, 23, 29, 32, 34, 39, 42, ... (OEIS A054504; Apostol 1976, p. 192).
such that the Mordell curve has no integer solutions are given by 6, 7, 11, 13, 14, 20, 21, 23, 29, 32, 34, 39, 42, ... (OEIS A054504; Apostol 1976, p. 192).
REFERENCES:
Apostol, T. M. Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
Cohen, H. " ." 24 Nov 2003. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0311&L=nmbrthry&F=&S=&P=1197.
." 24 Nov 2003. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0311&L=nmbrthry&F=&S=&P=1197.
Conrad, M. Untitled. https://emmy.math.uni-sb.de/~simath/MORDELL/MORDELL+.
Gebel, J. "Data on Mordell's Curve." https://tnt.math.metro-u.ac.jp/simath/MORDELL/.
Gebel, J.; Pethő, A.; and Zimmer, H. G. "On Mordell's Equation." Compos. Math. 110, 335-367, 1998.
Llorente, P. and Quer, J. "On the 3-Sylow Subgroup of the Class Group of Quadratic Fields." Math. Comput. 50, 321-333, 1988.
Mestre, J.-F. "Rang de courbes elliptiques d'invariant donné." C.R. Acad. Sci. Paris 314, 919-922, 1992.
Mestre, J.-F. "Rang de courbes elliptiques d'invariant nul." C.R. Acad. Sci. Paris 321, 1235-1236, 1995.
Metsaenkylae, T. "Catalan's Conjecture: Another Old Diophantine Problem Solved." Bull. Amer. Math. Soc. S 0273-0979(03)00993-5, September 5, 2003.
Mordell, L. J. Diophantine Equations. London: Academic Press, 1969.
Myerson, G. "Re:  ." 24 Nov 2003. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0311&L=nmbrthry&F=&S=&P=1290.
." 24 Nov 2003. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0311&L=nmbrthry&F=&S=&P=1290.
Quer, J. "Corps quadratiques de 3-rang 6 et courbes elliptiques de rang 12." C.R. Acad. Sci. Paris. Sér. 1 Math. 305, 215-218, 1987.
Sierpiński, W. and Schinzel, A. Elementary Theory of Numbers, 2nd Eng. ed. Amsterdam, Netherlands: North-Holland, 1988.
Sloane, N. J. A. Sequence A054504 in "The On-Line Encyclopedia of Integer Sequences."
Szymiczek, K. "Re:  ." 26 Nov 2003. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0311&L=nmbrthry&F=&S=&P=1492.
." 26 Nov 2003. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0311&L=nmbrthry&F=&S=&P=1492.
Uspensky, J. V. and Heaslet, M. A. Elementary Number Theory. New York: McGraw-Hill, 1939.
Wakulicz, A. "On the Equation 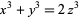 ." Colloq. Math. 5, 11-15, 1957.
." Colloq. Math. 5, 11-15, 1957.
Womack, T. "Minimal-Known Positive and Negative  for Mordell Curves of Given Rank." https://www.maths.nott.ac.uk/personal/pmxtow/mordellc.htm.
for Mordell Curves of Given Rank." https://www.maths.nott.ac.uk/personal/pmxtow/mordellc.htm.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


