


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-1-2021
Date: 4-2-2020
Date: 28-10-2019
|
A Mersenne number is a number of the form
 |
(1) |
where 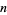 is an integer. The Mersenne numbers consist of all 1s in base-2, and are therefore binary repunits. The first few Mersenne numbers are 1, 3, 7, 15, 31, 63, 127, 255, ... (OEIS A000225), corresponding to
is an integer. The Mersenne numbers consist of all 1s in base-2, and are therefore binary repunits. The first few Mersenne numbers are 1, 3, 7, 15, 31, 63, 127, 255, ... (OEIS A000225), corresponding to 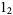 ,
, 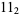 ,
, 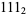 ,
, 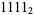 , ... in binary.
, ... in binary.
The Mersenne numbers are also the numbers obtained by setting 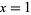 in a Fermat polynomial. They also correspond to Cunningham numbers
in a Fermat polynomial. They also correspond to Cunningham numbers 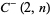 .
.
The number of digits 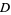 in the Mersenne number
in the Mersenne number 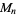 is
is
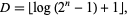 |
(2) |
where 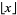 is the floor function, which, for large
is the floor function, which, for large 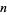 , gives
, gives
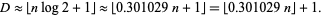 |
(3) |
The number of digits in 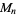 is the same as the number of digits in
is the same as the number of digits in 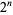 , namely 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, ... (OEIS A034887). The numbers of decimal digits in
, namely 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, ... (OEIS A034887). The numbers of decimal digits in 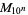 for
for 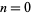 , 1, ... are given by 1, 4, 31, 302, 3011, 30103, 301030, 3010300, 30103000, 301029996, ... (OEIS A114475), which correspond to the decimal expansion of
, 1, ... are given by 1, 4, 31, 302, 3011, 30103, 301030, 3010300, 30103000, 301029996, ... (OEIS A114475), which correspond to the decimal expansion of 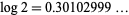 (OEIS A007524).
(OEIS A007524).
The numbers of prime factors of 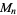 for
for 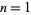 , 2, ... are 0, 1, 1, 2, 1, 3, 1, 3, 2, 3, 2, 5, 1, 3, 3, 4, 1, 6, ... (OEIS A046051), and the first few factorizations are
, 2, ... are 0, 1, 1, 2, 1, 3, 1, 3, 2, 3, 2, 5, 1, 3, 3, 4, 1, 6, ... (OEIS A046051), and the first few factorizations are
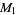 |
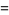 |
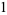 |
(4) |
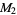 |
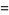 |
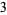 |
(5) |
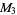 |
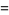 |
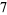 |
(6) |
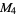 |
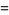 |
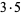 |
(7) |
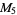 |
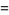 |
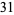 |
(8) |
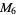 |
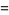 |
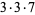 |
(9) |
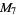 |
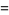 |
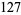 |
(10) |
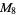 |
 |
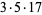 |
(11) |
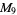 |
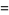 |
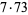 |
(12) |
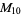 |
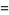 |
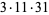 |
(13) |
(OEIS A001265). The smallest primes dividing 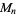 are therefore 1, 3, 7, 3, 31, 3, 127, 3, 7, 3, 23, 3, 8191, ... (OEIS A049479), and the largest are 1, 3, 7, 5, 31, 7, 127, 17, 73, 31, 89, 13, 8191, ... (OEIS A005420).
are therefore 1, 3, 7, 3, 31, 3, 127, 3, 7, 3, 23, 3, 8191, ... (OEIS A049479), and the largest are 1, 3, 7, 5, 31, 7, 127, 17, 73, 31, 89, 13, 8191, ... (OEIS A005420).
In order for the Mersenne number 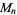 to be prime,
to be prime, 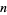 must be prime. This is true since for composite
must be prime. This is true since for composite 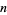 with factors
with factors 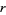 and
and 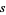 ,
, 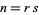 . Therefore,
. Therefore, 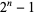 can be written as
can be written as 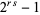 , which is a binomial number and can be factored. Since the most interest in Mersenne numbers arises from attempts to factor them, many authors prefer to define a Mersenne number as a number of the above form
, which is a binomial number and can be factored. Since the most interest in Mersenne numbers arises from attempts to factor them, many authors prefer to define a Mersenne number as a number of the above form
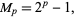 |
(14) |
but with 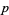 restricted to prime values.
restricted to prime values.
All known Mersenne numbers 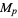 with
with 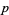 prime are squarefree. However, Guy (1994) believes that there are
prime are squarefree. However, Guy (1994) believes that there are 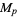 which are not squarefree.
which are not squarefree.
The search for Mersenne primes is one of the most computationally intensive and actively pursued areas of advanced and distributed computing. Edgington maintains a list of known factorizations of 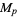 for prime
for prime 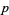 .
.
REFERENCES:
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 13, 2005.
Edgington, W. "Will Edgington's Mersenne Page." https://www.garlic.com/~wedgingt/mersenne.html.
Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, pp. 47-51, 2000.
Gardner, M. "Mathematical Games: About the Remarkable Similarity between the Icosian Game and the Towers of Hanoi." Sci. Amer. 196, 150-156, May 1957.
Guy, R. K. "Mersenne Primes. Repunits. Fermat Numbers. Primes of Shape 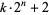 [sic]." §A3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 8-13, 1994.
[sic]." §A3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 8-13, 1994.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 15-16 and 22, 1979.
Pappas, T. "Mersenne's Number." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 211, 1989.
Robinson, R. M. "Mersenne and Fermat Numbers." Proc. Amer. Math. Soc. 5, 842-846, 1954.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 14, 18-19, 22, and 29-30, 1993.
Sloane, N. J. A. Sequences A000225/M2655, A001265, A005420/M2609, A007524/M2196, A034887, A046051, A049479, and A114475 in "The On-Line Encyclopedia of Integer Sequences."
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 23-24, 1999.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|