
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2020
Date: 23-1-2020
Date: 20-2-2020
|
The Dedekind 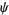 -function is defined by the divisor product
-function is defined by the divisor product
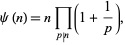 |
(1) |
where the product is over the distinct prime factors of 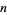 , with the special case
, with the special case 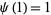 . The first few values are
. The first few values are
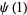 |
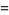 |
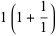 |
(2) |
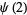 |
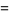 |
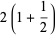 |
(3) |
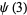 |
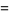 |
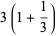 |
(4) |
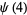 |
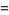 |
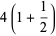 |
(5) |
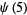 |
 |
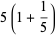 |
(6) |
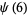 |
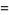 |
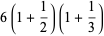 |
(7) |
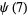 |
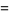 |
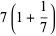 |
(8) |
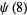 |
 |
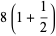 |
(9) |
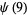 |
 |
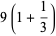 |
(10) |
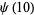 |
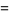 |
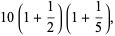 |
(11) |
giving 1, 3, 4, 6, 6, 12, 8, 12, 12, 18, ... (OEIS A001615).
Sums for 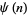 include
include
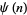 |
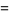 |
![sum_(d|n)n([mu(d)]^2)/d](https://mathworld.wolfram.com/images/equations/DedekindFunction/Inline37.gif) |
 |
 |
(12) |
 |
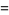 |
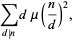 |
(13) |
where 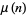 is the Möbius function.
is the Möbius function.
The Dirichlet generating function is given by
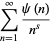 |
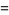 |
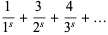 |
(14) |
 |
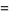 |
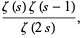 |
(15) |
where 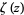 is the Riemann zeta function.
is the Riemann zeta function.
REFERENCES:
Cox, D. A. Primes of the Form x2+ny2: Fermat, Class Field Theory and Complex Multiplication. New York: Wiley, p. 228, 1997.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 96, 1994.
Sloane, N. J. A. Sequence A001615/M2315 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|