

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Tau Function
المؤلف:
Andrews, G. E.; Berndt, B. C.; and Rankin, R. A.
المصدر:
Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June 1-5, 1987 New York: Academic Press, 1988.
الجزء والصفحة:
...
22-8-2020
1433
Tau Function
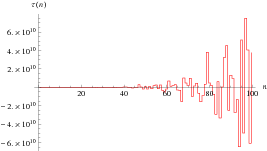
A function 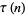 related to the divisor function
related to the divisor function 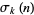 , also sometimes called Ramanujan's tau function. It is defined via the Fourier series of the modular discriminant
, also sometimes called Ramanujan's tau function. It is defined via the Fourier series of the modular discriminant 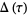 for
for 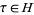 , where
, where 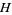 is the upper half-plane, by
is the upper half-plane, by
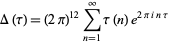 |
(1) |
(Apostol 1997, p. 20). The tau function is also given by the Cauchy product
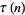 |
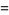 |
(2) |
|
 |
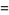 |
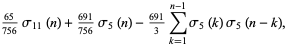 |
(3) |
where 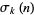 is the divisor function (Apostol 1997, pp. 24 and 140),
is the divisor function (Apostol 1997, pp. 24 and 140), 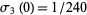 , and
, and 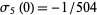 .
.
The tau function has generating function
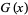 |
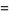 |
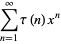 |
(4) |
 |
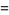 |
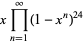 |
(5) |
 |
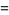 |
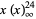 |
(6) |
 |
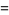 |
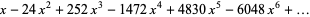 |
(7) |
 |
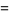 |
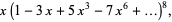 |
(8) |
where 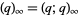 is a q-Pochhammer symbol. The first few values are 1,
is a q-Pochhammer symbol. The first few values are 1, 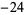 , 252,
, 252, 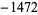 , 4830, ... (OEIS A000594). The tau function is given by the Wolfram Language function RamanujanTau[n].
, 4830, ... (OEIS A000594). The tau function is given by the Wolfram Language function RamanujanTau[n].
The series
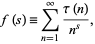 |
(9) |
is known as the tau Dirichlet series.
Lehmer (1947) conjectured that 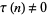 for all
for all 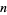 , an assertion sometimes known as Lehmer's conjecture. Lehmer verified the conjecture for
, an assertion sometimes known as Lehmer's conjecture. Lehmer verified the conjecture for 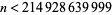 (Apostol 1997, p. 22). The following table summarizes progress on finding successively larger values of
(Apostol 1997, p. 22). The following table summarizes progress on finding successively larger values of 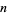 for which this condition holds.
for which this condition holds.
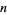 |
reference |
| 3316799 | Lehmer (1947) |
| 214928639999 | Lehmer (1949) |
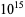 |
Serre (1973, p. 98), Serre (1985) |
| 1213229187071998 | Jennings (1993) |
| 22689242781695999 | Jordan and Kelly (1999) |
| 22798241520242687999 | Bosman (2007) |
Ramanujan gave the computationally efficient triangular recurrence formula
![(n-1)tau(n)=sum_(m=1)^(b_n)(-1)^(m+1)(2m+1)×[n-1-9/2m(m+1)]tau(n-1/2m(m+1)),](https://mathworld.wolfram.com/images/equations/TauFunction/NumberedEquation3.gif) |
(10) |
where
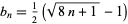 |
(11) |
(Lehmer 1943; Jordan and Kelly 1999), which can be used recursively with the formula
![tau(p^n)=sum_(j=0)^(|_n/2_|)(-1)^j(n-j; n-2j)p^(11j)[tau(p)]^(n-2j)](https://mathworld.wolfram.com/images/equations/TauFunction/NumberedEquation5.gif) |
(12) |
(Gandhi 1961, Jordan and Kelly 1999).
Ewell (1999) gave the beautiful formulas
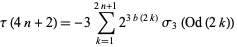 |
(13) |
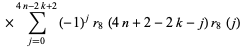 |
(14) |
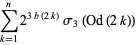 |
(15) |
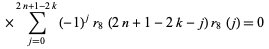 |
(16) |
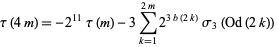 |
(17) |
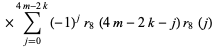 |
(18) |
![tau(2n+1)=sum_(k=1)^(2n+1)2^(3[b(2k)-1])sigma_3(Od(2k))](https://mathworld.wolfram.com/images/equations/TauFunction/Inline45.gif) |
(19) |
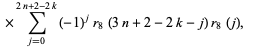 |
(20) |
where 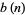 is the exponent of the exact power of 2 dividing
is the exponent of the exact power of 2 dividing 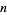 ,
, 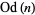 is the odd part of
is the odd part of 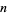 ,
, 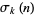 is the divisor function of
is the divisor function of 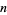 , and
, and 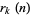 is the sum of squares function.
is the sum of squares function.
For prime 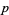 ,
,
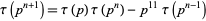 |
(21) |
for 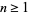 , and
, and
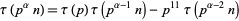 |
(22) |
for 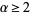 and
and 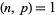 (Mordell 1917; Apostol 1997, p. 92).
(Mordell 1917; Apostol 1997, p. 92).
Ramanujan conjectured and Mordell (1917) proved that if 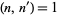 , then
, then
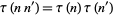 |
(23) |
(Hardy 1999, p. 161). More generally,
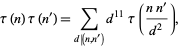 |
(24) |
which reduces to the first form if 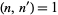 (Mordell 1917; Apostol 1997, p. 93).
(Mordell 1917; Apostol 1997, p. 93).
Ramanujan (1920) showed that
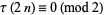 |
(25) |
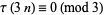 |
(26) |
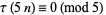 |
(27) |
(Darling 1921; Wilton 1930),
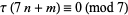 |
(28) |
for 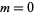 or one the quadratic non-residues of 7, i.e., 3, 5, 6, and
or one the quadratic non-residues of 7, i.e., 3, 5, 6, and
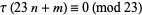 |
(29) |
for one the quadratic non-residues of 23, i.e., 5, 7, 10, 11, 14, 15, 17, 19, 20, 21, 22 (Mordell 1922; Wilton 1930). Ewell (1999) showed that
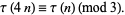 |
(30) |
Ramanujan conjectured and Watson proved that 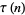 is divisible by 691 for almost all
is divisible by 691 for almost all 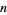 , specifically
, specifically
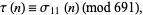 |
(31) |
where 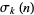 is the divisor function (Wilton 1930; Apostol 1997, pp. 93 and 140; Jordan and Kelly 1999), and 691 is the numerator of the Bernoulli number
is the divisor function (Wilton 1930; Apostol 1997, pp. 93 and 140; Jordan and Kelly 1999), and 691 is the numerator of the Bernoulli number 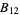 .
.
Additional congruences include
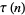 |
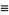 |
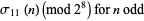 |
(32) |
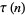 |
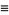 |
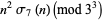 |
(33) |
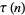 |
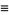 |
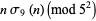 |
(34) |
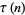 |
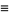 |
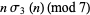 |
(35) |
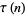 |
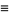 |
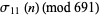 |
(36) |
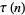 |
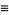 |
(37) |
|
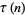 |
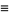 |
(38) |
|
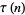 |
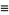 |
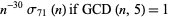 |
(39) |
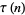 |
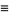 |
(40) |
|
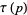 |
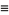 |
(41) |
where 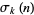 is the divisor function (Swinnerton-Dyer 1988, Jordan and Kelly 1999).
is the divisor function (Swinnerton-Dyer 1988, Jordan and Kelly 1999).
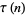 is almost always divisible by
is almost always divisible by 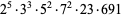 according to Ramanujan. In fact, Serre has shown that
according to Ramanujan. In fact, Serre has shown that 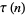 is almost always divisible by any integer (Andrews et al. 1988).
is almost always divisible by any integer (Andrews et al. 1988).
The summatory tau function is given by
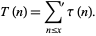 |
(42) |
Here, the prime indicates that when  is an integer, the last term
is an integer, the last term 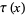 should be replaced by
should be replaced by 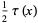 .
.
REFERENCES:
Andrews, G. E.; Berndt, B. C.; and Rankin, R. A. (Eds.). Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June 1-5, 1987 New York: Academic Press, 1988.
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, 1997.
Charles, C. D. "Computing the Ramanujan Tau Function." https://www.cs.wisc.edu/~cdx/.
Darling, H. B. C. Proc. London Math. Soc. 19, 350-372, 1921.
Ewell, J. A. "New Representations of Ramanujan's Tau Function." Proc. Amer. Math. Soc. 128, 723-726, 1999.
Gandhi, J. M. "The Nonvanishing of Ramanujan's  -Function." Amer. Math. Monthly 68, 757-760, 1961.
-Function." Amer. Math. Monthly 68, 757-760, 1961.
Hardy, G. H. "Ramanujan's Function 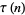 ." Ch. 10 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 63 and 161-185, 1999.
." Ch. 10 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 63 and 161-185, 1999.
Jennings, D. Ph.D. thesis. Southampton, 1993.
Jordan, B. and Kelly, B. III. "The Vanishing of the Ramanujan Tau Function." Preprint, 12 Mar 1999.
Keiper, J. "On the Zeros of the Ramanujan  -Dirichlet Series in the Critical Strip." Math. Comput. 65, 1613-1619, 1996.
-Dirichlet Series in the Critical Strip." Math. Comput. 65, 1613-1619, 1996.
LeVeque, W. J. §F35 in Reviews in Number Theory 1940-1972. Providence, RI: Amer. Math. Soc., 1974.
Lehmer, D. H. "Ramanujan's Function 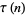 ." Duke Math. J. 10, 483-492, 1943.
." Duke Math. J. 10, 483-492, 1943.
Lehmer, D. H. "The Vanishing of Ramanujan's Function 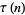 ." Duke Math. J. 14, 429-433, 1947.
." Duke Math. J. 14, 429-433, 1947.
Moreno, C. J. "A Necessary and Sufficient Condition for the Riemann Hypothesis for Ramanujan's Zeta Function." Illinois J. Math. 18, 107-114, 1974.
Mordell, L. J. "On Mr. Ramanujan's Empirical Expansions of Modular Functions." Proc. Cambridge Phil. Soc. 19, 117-124, 1917.
Mordell, L. J. "Note on Certain Modular Relations Considered by Messrs Ramanujan, Darling, and Rogers." Proc. London Math. Soc. 20, 408-416, 1922.
Ramanujan, S. Proc. London Math. Soc. 18, 1920.
Ramanujan, S. "Congruence Properties of Partitions." Math. Z. 9, 147-153, 1921.
Serre, J.-P. A Course in Arithmetic. New York: Springer-Verlag, 1973.
Serre, J.-P. "Sur la Lacunatité des Puissances de 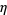 ." Glasgow Math. J. 27, 203-221, 1985.
." Glasgow Math. J. 27, 203-221, 1985.
Sivaramakrishnan, R. Classical Theory of Arithmetic Functions. New York: Dekker, pp. 275-278, 1989.
Sloane, N. J. A. Sequence A000594/M5153 in "The On-Line Encyclopedia of Integer Sequences."
Spira, R. "Calculation of the Ramanujan Tau-Dirichlet Series." Math. Comput. 27, 379-385, 1973.
Stanley, G. K. "Two Assertions Made by Ramanujan." J. London Math. Soc. 3, 232-237, 1928.
Stanley, G. K. Corrigendum to "Two Assertions Made by Ramanujan." J. London Math. Soc. 4, 32, 1929.
Swinnerton-Dyer, H. P. F. "Congruence Properties of 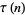 ." In Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and R. A. Rankin). New York: Academic Press, 1988.
." In Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and R. A. Rankin). New York: Academic Press, 1988.
Watson, G. N. "Über Ramanujansche Kongruenzeigenschaften der Zerfällungsanzahlen." Math. Z. 39, 712-731, 1935.
Wilton, J. R. "Congruence Properties of Ramanujan's Function 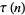 ." Proc. London Math. Soc. 31, 1-17, 1930.
." Proc. London Math. Soc. 31, 1-17, 1930.
Yoshida, H. "On Calculations of Zeros of L-Functions Related with Ramanujan's Discriminant Function on the Critical Line." J. Ramanujan Math. Soc. 3, 87-95, 1988.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















