

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Prime Counting Function
المؤلف:
Baugh, D. and Walisch, K.
المصدر:
"New Confirmed pi(1027) Prime Counting Function Record
الجزء والصفحة:
...
26-8-2020
1437
Prime Counting Function

The prime counting function is the function 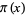 giving the number of primes less than or equal to a given number
giving the number of primes less than or equal to a given number  (Shanks 1993, p. 15). For example, there are no primes
(Shanks 1993, p. 15). For example, there are no primes 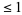 , so
, so 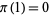 . There is a single prime (2)
. There is a single prime (2) 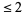 , so
, so 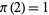 . There are two primes (2 and 3)
. There are two primes (2 and 3) 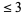 , so
, so 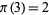 . And so on.
. And so on.
The notation 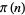 for the prime counting function is slightly unfortunate because it has nothing whatsoever to do with the constant
for the prime counting function is slightly unfortunate because it has nothing whatsoever to do with the constant 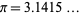 . This notation was introduced by number theorist Edmund Landau in 1909 and has now become standard. In the words of Derbyshire (2004, p. 38), "I am sorry about this; it is not my fault. You'll just have to put up with it."
. This notation was introduced by number theorist Edmund Landau in 1909 and has now become standard. In the words of Derbyshire (2004, p. 38), "I am sorry about this; it is not my fault. You'll just have to put up with it."
Letting 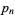 denote the
denote the 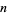 th prime,
th prime,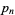 is a right inverse of
is a right inverse of 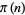 since
since
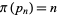 |
(1) |
for all positive integers. Also,
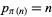 |
(2) |
iff 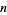 is a prime number.
is a prime number.
The first few values of 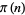 for
for 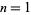 , 2, ... are 0, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6, 6, 6, ... (OEIS A000720). The Wolfram Language command giving the prime counting function for a number
, 2, ... are 0, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6, 6, 6, ... (OEIS A000720). The Wolfram Language command giving the prime counting function for a number  is PrimePi[x], which works up to a maximum value of
is PrimePi[x], which works up to a maximum value of 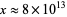 .
.
The notation 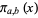 is used to denote the modular prime counting function, i.e., the number of primes of the form
is used to denote the modular prime counting function, i.e., the number of primes of the form 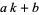 less than or equal to
less than or equal to  (Shanks 1993, pp. 21-22).
(Shanks 1993, pp. 21-22).
The following table gives the values of 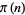 for powers of 10 (OEIS A006880), extending other printed tabulations (e.g., Hardy and Wright 1979, p. 4; Shanks 1993, pp. 242-243; Ribenboim 1996, p. 237; Derbyshire 2004, p. 35). Note that
for powers of 10 (OEIS A006880), extending other printed tabulations (e.g., Hardy and Wright 1979, p. 4; Shanks 1993, pp. 242-243; Ribenboim 1996, p. 237; Derbyshire 2004, p. 35). Note that 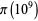 was incorrectly computed as
was incorrectly computed as 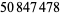 by Meissel (1885), which is off by 56 (Havil 2003, p. 171), a result quoted by Hardy and Wright (1979) and Hardy (1999) and sometimes (erroneously) known as Bertelsen's number. The value for
by Meissel (1885), which is off by 56 (Havil 2003, p. 171), a result quoted by Hardy and Wright (1979) and Hardy (1999) and sometimes (erroneously) known as Bertelsen's number. The value for 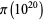 comes from Deleglise and Rivat (1996), and
comes from Deleglise and Rivat (1996), and 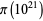 was reported by X. Gourdon on Oct. 27, 2000. Oliveira e Silva and X. Gourdon independently computed values for
was reported by X. Gourdon on Oct. 27, 2000. Oliveira e Silva and X. Gourdon independently computed values for 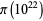 and
and 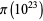 , but an error was found in the computations of Gourdon. The value given for
, but an error was found in the computations of Gourdon. The value given for 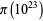 was computed by Tomás Oliveira e Silva, who verified this result using set sets of hardware and program parameters (pers. comm., Apr. 7, 2008). (Values of
was computed by Tomás Oliveira e Silva, who verified this result using set sets of hardware and program parameters (pers. comm., Apr. 7, 2008). (Values of 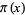 computed independently by Oliveira e Silva and X. Gourdon already agree for all powers of 10 up to
computed independently by Oliveira e Silva and X. Gourdon already agree for all powers of 10 up to 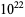 .)
.) 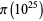 was computed by Büthe (2014),
was computed by Büthe (2014), 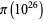 by Staple in 2014 (Staple 2015), and
by Staple in 2014 (Staple 2015), and 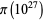 by D. Baugh and K. Walisch (2015) using the primecount fast prime counting function implementation (Walisch).
by D. Baugh and K. Walisch (2015) using the primecount fast prime counting function implementation (Walisch).
 |
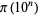 |
reference |
| 1 | 4 | antiquity |
| 2 | 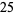 |
L. Pisano (1202; Beiler) |
| 3 | 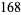 |
F. van Schooten (1657; Beiler) |
| 4 | 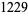 |
F. van Schooten (1657; Beiler) |
| 5 | 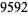 |
T. Brancker (1668; Beiler) |
| 6 | 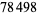 |
A. Felkel (1785; Beiler) |
| 7 | 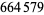 |
J. P. Kulik (1867; Beiler) |
| 8 | 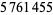 |
Meissel (1871; corrected) |
| 9 | 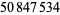 |
Meissel (1886; corrected) |
| 10 | 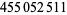 |
Lehmer (1959; corrected) |
| 11 | 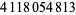 |
Bohmann (1972; corrected) |
| 12 | 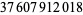 |
|
| 13 | 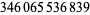 |
|
| 14 | 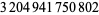 |
Lagarias et al. (1985) |
| 15 | 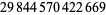 |
Lagarias et al. (1985) |
| 16 | 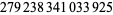 |
Lagarias et al. (1985) |
| 17 | 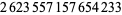 |
M. Deleglise and J. Rivat (1994) |
| 18 | 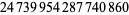 |
Deleglise and Rivat (1996) |
| 19 | 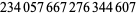 |
M. Deleglise (June 19, 1996) |
| 20 | 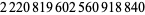 |
M. Deleglise (June 19, 1996) |
| 21 | 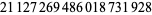 |
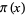 project (Dec. 2000) project (Dec. 2000) |
| 22 | 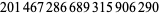 |
P. Demichel and X. Gourdon (Feb. 2001) |
| 23 | 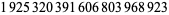 |
T. Oliveira e Silva (pers. comm., Apr. 7, 2008) |
| 24 | 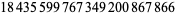 |
Platt |
| 25 | 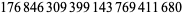 |
Büthe (2014) |
| 26 | 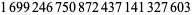 |
Staple (2015) |
| 27 | 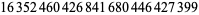 |
D. Baugh and K. Walisch (2015) |
One of the most fundamental and important results in number theory is the asymptotic form of 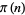 as
as 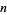 becomes large. This is given by the prime number theorem, which states that
becomes large. This is given by the prime number theorem, which states that
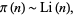 |
(3) |
where 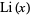 is the logarithmic integral and
is the logarithmic integral and 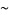 is asymptotic notation. This relation was first postulated by Gauss in 1792 (when he was 15 years old), although not revealed until an 1849 letter to Johann Encke and not published until 1863 (Gauss 1863; Havil 2003, pp. 176-177).
is asymptotic notation. This relation was first postulated by Gauss in 1792 (when he was 15 years old), although not revealed until an 1849 letter to Johann Encke and not published until 1863 (Gauss 1863; Havil 2003, pp. 176-177).
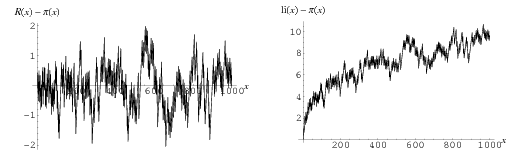
The following table compares the prime counting function 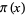 , Riemann prime counting function
, Riemann prime counting function 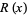 , and logarithmic integral
, and logarithmic integral 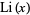 for powers of ten, i.e.,
for powers of ten, i.e., 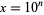 . The corresponding differences are plotted above for small
. The corresponding differences are plotted above for small  . Note that the values given by Hardy (1999, p. 26) for
. Note that the values given by Hardy (1999, p. 26) for 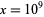 are incorrect. In the following table,
are incorrect. In the following table, ![[x]](https://mathworld.wolfram.com/images/equations/PrimeCountingFunction/Inline75.gif) denotes the nearest integer function. A similar table comparing
denotes the nearest integer function. A similar table comparing 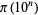 and
and 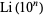 is given by Borwein and Bailey (2003, p. 65).
is given by Borwein and Bailey (2003, p. 65).
| Sloane | A057794 | A057752 |
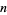 |
![[pi(10^n)-R(10^n)]](https://mathworld.wolfram.com/images/equations/PrimeCountingFunction/Inline79.gif) |
![[pi(10^n)-Li(10^n)]](https://mathworld.wolfram.com/images/equations/PrimeCountingFunction/Inline80.gif) |
| 1 | 1 | 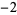 |
| 2 | 1 | 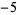 |
| 3 | 0 | 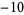 |
| 4 | 2 | 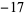 |
| 5 | 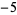 |
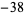 |
| 6 | 29 | 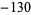 |
| 7 | 88 | 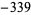 |
| 8 | 97 | 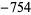 |
| 9 | 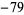 |
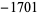 |
| 10 | 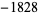 |
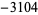 |
| 11 | 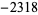 |
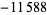 |
| 12 | 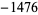 |
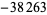 |
| 13 | 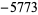 |
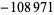 |
| 14 | 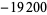 |
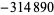 |
| 15 | 73218 | 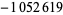 |
| 16 | 327052 | 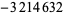 |
| 17 | 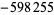 |
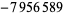 |
| 18 | 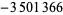 |
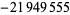 |
| 19 | 23884333 | 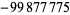 |
| 20 | 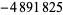 |
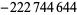 |
| 21 | 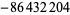 |
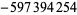 |
| 22 | 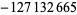 |
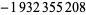 |
The prime counting function can be expressed by Legendre's formula, Lehmer's formula, Mapes' method, or Meissel's formula. A brief history of attempts to calculate 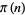 is given by Berndt (1994). The following table is taken from Riesel (1994), where
is given by Berndt (1994). The following table is taken from Riesel (1994), where 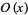 is asymptotic notation.
is asymptotic notation.
| method | time complexity | storage complexity |
| Lagarias-Miller-Odlyzko | 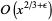 |
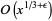 |
| Lagarias-Odlyzko 1 | 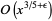 |
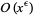 |
| Lagarias-Odlyzko 2 | 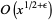 |
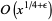 |
| Legendre's formula | 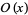 |
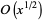 |
| Lehmer | 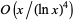 |
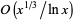 |
| Mapes' method | 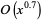 |
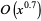 |
| Meissel | 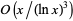 |
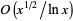 |
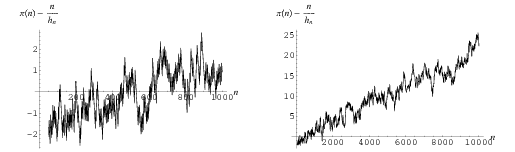
An approximate formula due to Locker-Ernst (Locker-Ernst 1959; Panaitopol 1999; Havil 2003, pp. 179-180), illustrated above, is given by
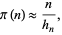 |
(4) |
where 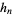 is related to the harmonic number
is related to the harmonic number 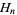 by
by 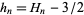 . This formula is within
. This formula is within 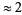 of the actual value for
of the actual value for 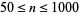 . The values for which
. The values for which 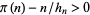 are 1, 109, 113, 114, 199, 200, 201, ... (OEIS A051046). Panaitopol (1999) shows that this quantity is positive for all
are 1, 109, 113, 114, 199, 200, 201, ... (OEIS A051046). Panaitopol (1999) shows that this quantity is positive for all 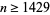 .
.
An upper bound for 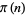 is given by
is given by
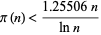 |
(5) |
for 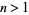 , and a lower bound by
, and a lower bound by
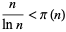 |
(6) |
for 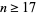 (Rosser and Schoenfeld 1962).
(Rosser and Schoenfeld 1962).
Hardy and Wright (1979, p. 414) give the formula
![pi(n)=-1+sum_(j=3)^n[(j-2)!-j|_((j-2)!)/j_|]](https://mathworld.wolfram.com/images/equations/PrimeCountingFunction/NumberedEquation7.gif) |
(7) |
for 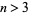 , where
, where 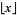 is the floor function.
is the floor function.
A modified version of the prime counting function is given by
|
(8) |
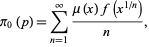 |
(9) |
where 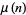 is the Möbius function and
is the Möbius function and 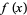 is the Riemann prime counting function.
is the Riemann prime counting function.
Ramanujan also showed that
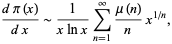 |
(10) |
where 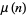 is the Möbius function (Berndt 1994, p. 117; Havil 2003, p. 199).
is the Möbius function (Berndt 1994, p. 117; Havil 2003, p. 199).
The smallest  such that
such that 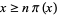 for
for 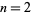 , 3, ... are 2, 27, 96, 330, 1008, ... (OEIS A038625), and the corresponding
, 3, ... are 2, 27, 96, 330, 1008, ... (OEIS A038625), and the corresponding 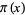 are 1, 9, 24, 66, 168, 437, ... (OEIS A038626). The number of solutions of
are 1, 9, 24, 66, 168, 437, ... (OEIS A038626). The number of solutions of 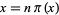 for
for 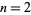 , 3, ... are 4, 3, 3, 6, 7, 6, ... (OEIS A038627).
, 3, ... are 4, 3, 3, 6, 7, 6, ... (OEIS A038627).
Ramanujan showed that for sufficiently large  ,
,
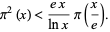 |
(11) |
This holds for 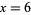 , 9, 10, 12, 14, 15, 16, 18, ... (OEIS A091886). The largest known prime for which the inequality fails is
, 9, 10, 12, 14, 15, 16, 18, ... (OEIS A091886). The largest known prime for which the inequality fails is 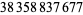 (Berndt 1994, pp. 112-113). The related inequality
(Berndt 1994, pp. 112-113). The related inequality
![[li(x)]^2<(ex)/(lnx)li(x/e)](https://mathworld.wolfram.com/images/equations/PrimeCountingFunction/NumberedEquation12.gif) |
(12) |
where
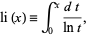 |
(13) |
is true for 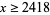 and no smaller number (Berndt 1994, p. 114).
and no smaller number (Berndt 1994, p. 114).
REFERENCES:
Baugh, D. and Walisch, K. "New Confirmed pi(1027) Prime Counting Function Record." https://www.mersenneforum.org/showthread.php?t=20473. Sep. 6, 2015.
Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, p. 218, 1966.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 134-135, 1994.
Booker, A. "The Nth Prime Page." https://primes.utm.edu/nthprime/.
Borwein, J. and Bailey, D. "Prime Numbers and the Zeta Function." Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 63-72, 2003.
Brent, R. P. "Irregularities in the Distribution of Primes and Twin Primes." Math. Comput. 29, 43-56, 1975.
Büthe, J. "A Practical Analytic Method for Calculating 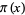 II." 26 Oct 2014. https://arxiv.org/abs/1410.7008.
II." 26 Oct 2014. https://arxiv.org/abs/1410.7008.
Caldwell, C. "How Many Primes Are There?" https://primes.utm.edu/howmany.shtml.
Deleglise, M. and Rivat, J. "Computing 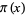 : The Meissel, Lehmer, Lagarias, Miller, Odlyzko Method." Math. Comput. 65, 235-245, 1996.
: The Meissel, Lehmer, Lagarias, Miller, Odlyzko Method." Math. Comput. 65, 235-245, 1996.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Finch, S. R. "Hardy-Littlewood Constants." §2.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 84-94, 2003.
Forbes, T. "Prime 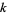 -tuplets." https://anthony.d.forbes.googlepages.com/ktuplets.htm.
-tuplets." https://anthony.d.forbes.googlepages.com/ktuplets.htm.
Gauss, C. F. Werke, Band 10, Teil I. p. 10, 1863.
Gourdon, X. "New Record Computation for pi(x), x=10^21." 27 Oct 2000. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0010&L=nmbrthry&P=2988.
Guiasu, S. "Is There Any Regularity in the Distribution of Prime Numbers at the Beginning of the Sequence of Positive Integers?" Math. Mag. 68, 110-121, 1995.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 164-188, 2003.
Lagarias, J.; Miller, V. S.; and Odlyzko, A. "Computing 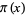 : The Meissel-Lehmer Method." Math. Comput. 44, 537-560, 1985.
: The Meissel-Lehmer Method." Math. Comput. 44, 537-560, 1985.
Lagarias, J. and Odlyzko, A. "Computing 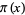 : An Analytic Method." J. Algorithms 8, 173-191, 1987.
: An Analytic Method." J. Algorithms 8, 173-191, 1987.
Locker-Ernst, L. "Bemerkung über die Verteilung der Primzahlen." Elemente Math. (Basel) 14, 1-5, 1959.
Mapes, D. C. "Fast Method for Computing the Number of Primes Less than a Given Limit." Math. Comput. 17, 179-185, 1963.
Meissel, E. D. F. "Über die Bestimmung der Primzahlmenge innerhalb gegebener Grenzen." Math. Ann. 2, 636-642, 1870.
Meissel, E. D. F. "Berechnung der Menge von Primzahlen, welche innerhalb der ersten Milliarde naturlicher Zahlen vorkommen." Math. Ann. 25, 251-257, 1885.
Nagell, T. "The Function 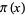 ." §16 in Introduction to Number Theory. New York: Wiley, pp. 54-57, 1951.
." §16 in Introduction to Number Theory. New York: Wiley, pp. 54-57, 1951.
Panaitopol, L. "Several Approximations of 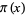 ." Math. Ineq. Appl. 2, 317-324, 1999.
." Math. Ineq. Appl. 2, 317-324, 1999.
Platt, D. "Computing 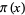 Analytically." To appear in Math. Comput.
Analytically." To appear in Math. Comput.
Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, 1996.
Riesel, H. "The Number of Primes Below  ." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 10-12, 1994.
." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 10-12, 1994.
Rosser, J. B. and Schoenfeld, L. "Approximate Formulas for Some Functions of Prime Numbers." Illinois J. Math. 6, 64-97, 1962.
Séroul, R. "The Function pi( )." §8.7 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 175-181, 2000.
)." §8.7 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 175-181, 2000.
Shallit, J. https://www.math.uwaterloo.ca/~shallit/bib/pi.bib.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, 1993.
Sloane, N. J. A. Sequences A000720/M0256, A006880/M3608, A038625, A038626, A038627, A052434, A052435, A057752, A057794, and A091886 in "The On-Line Encyclopedia of Integer Sequences."
Staple, D. B. "The Combinatorial Algorithm for Computing 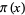 ." https://arxiv.org/abs/1503.01839. 28 May 2015.
." https://arxiv.org/abs/1503.01839. 28 May 2015.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 74-76, 1991.
Walisch, K. "Fast Prime Counting Function Implementations." https://github.com/kimwalisch/primecount.
Wolf, M. "Unexpected Regularities in the Distribution of Prime Numbers." https://www.ift.uni.wroc.pl/~mwolf/.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















