


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-12-2020
Date: 26-11-2020
Date: 18-1-2021
|
A sequence of primes 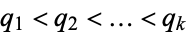 is a Cunningham chain of the first kind (second kind) of length
is a Cunningham chain of the first kind (second kind) of length 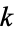 if
if 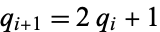 (
(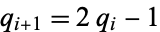 ) for
) for 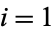 , ...,
, ..., 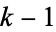 . Cunningham primes of the first kind are Sophie Germain primes.
. Cunningham primes of the first kind are Sophie Germain primes.
It is conjectured there are arbitrarily long Cunningham chains. The longest known Cunningham chains are of length 17, with the first examples found corresponding to 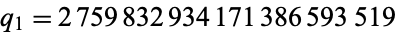 (first kind; J. Wroblewski, May 2008) and
(first kind; J. Wroblewski, May 2008) and 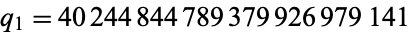 (second kind; J. Wroblewski, Jun. 2008).
(second kind; J. Wroblewski, Jun. 2008).
The smallest prime beginning a complete Cunningham chain of the first kind of lengths 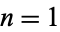 , 2, ... are 13, 3, 41, 509, 2, 89, 1122659, 19099919, 85864769, 26089808579, ... (OEIS A005602).
, 2, ... are 13, 3, 41, 509, 2, 89, 1122659, 19099919, 85864769, 26089808579, ... (OEIS A005602).
The smallest prime beginning a complete Cunningham chain of the second kind of lengths 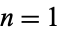 , 2, ... are 11, 7, 2, 2131, 1531, 33301, 16651, 15514861, 857095381, 205528443121, ... (OEIS A005603).
, 2, ... are 11, 7, 2, 2131, 1531, 33301, 16651, 15514861, 857095381, 205528443121, ... (OEIS A005603).
REFERENCES:
Augustin, D. "Cunningham Chain Records." Dec. 30, 2008. https://hjem.get2net.dk/jka/math/Cunningham_Chain_records.htm.
Caldwell, C. "The Top Twenty: Cunningham Chain (1st Kind)." https://primes.utm.edu/top20/page.php?id=19.
Caldwell, C. "The Top Twenty: Cunningham Chain (2nd Kind)." https://primes.utm.edu/top20/page.php?id=20.
Forbes, T. "Prime Clusters and Cunningham Chains." Math. Comput. 68, 1739-1748, 1999.
Guy, R. K. "Cunningham Chains." §A7 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 18-19, 1994.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, p. 333, 1996.
Sloane, N. J. A. Sequences A005602 and A005603 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|