
Lucky Number of Euler
 المؤلف:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H
المؤلف:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H
 المصدر:
Experimental Mathematics in Action. Wellesley, MA: A K Peters
المصدر:
Experimental Mathematics in Action. Wellesley, MA: A K Peters
 الجزء والصفحة:
...
الجزء والصفحة:
...
 8-9-2020
8-9-2020
 3095
3095
Lucky Number of Euler
A lucky number of Euler is a number 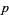 such that the prime-generating polynomial
such that the prime-generating polynomial
is prime for 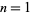 , 2, ...,
, 2, ..., 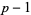 . Such numbers are related to the imaginary quadratic field in which the ring of integers is factorable. Specifically, the lucky numbers of Euler (excluding the trivial case
. Such numbers are related to the imaginary quadratic field in which the ring of integers is factorable. Specifically, the lucky numbers of Euler (excluding the trivial case 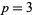 ) are those numbers
) are those numbers 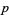 such that the imaginary quadratic field
such that the imaginary quadratic field 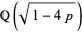 has class number 1 (Rabinowitz 1913, Le Lionnais 1983, Conway and Guy 1996, Ribenboim 2000).
has class number 1 (Rabinowitz 1913, Le Lionnais 1983, Conway and Guy 1996, Ribenboim 2000).
As proved by Heegner (1952)--although his proof was not accepted as complete at the time--and subsequently established by Stark (1967), there are only nine numbers 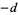 such that
such that 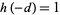 (the Heegner numbers
(the Heegner numbers 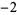 ,
, 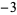 ,
, 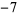 ,
, 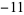 ,
, 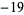 ,
, 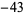 ,
, 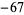 , and
, and 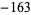 ), and of these, only 7, 11, 19, 43, 67, and 163 are of the required form. Therefore, the only lucky numbers of Euler are 2, 3, 5, 11, 17, and 41 (Le Lionnais 1983, OEIS A014556), and there does not exist a better prime-generating polynomial of Euler's form.
), and of these, only 7, 11, 19, 43, 67, and 163 are of the required form. Therefore, the only lucky numbers of Euler are 2, 3, 5, 11, 17, and 41 (Le Lionnais 1983, OEIS A014556), and there does not exist a better prime-generating polynomial of Euler's form.
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, p. 13, 2007.
Conway, J. H. and Guy, R. K. "The Nine Magic Discriminants." In The Book of Numbers. New York: Springer-Verlag, pp. 224-226, 1996.
Heegner, K. "Diophantische Analysis und Modulfunktionen." Math. Z. 56, 227-253, 1952.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 88 and 144, 1983.
Meyer, C. "Bemerkungen zum Satz von Heegner-Stark über die imaginär-quadratischen Zahlkörper mit der Klassenzahl Eins." J. reine angew. Math. 242, 179-214, 1970.
Rabinowitz, G. "Eindeutigkeit der Zerlegung in Primzahlfaktoren in quadratischen Zahlkörpern." Proc. Fifth Internat. Congress Math. (Cambridge) 1, 418-421, 1913.
Ribenboim, P. My Numbers, My Friends. New York: Springer-Verlag, 2000.
Sloane, N. J. A. Sequence A014556 in "The On-Line Encyclopedia of Integer Sequences."
Stark, H. M. "A Complete Determination of the Complex Quadratic Fields of Class Number One." Michigan Math. J. 14, 1-27, 1967.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


