
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-12-2019
Date: 29-1-2020
Date: 16-10-2019
|
A deeper result than the Hardy-Ramanujan theorem. Let 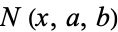 be the number of integers in
be the number of integers in ![[n,x]](https://mathworld.wolfram.com/images/equations/Erdos-KacTheorem/Inline2.gif) such that inequality
such that inequality
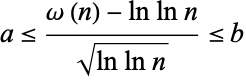 |
(1) |
holds, where 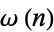 is the number of distinct prime factors of
is the number of distinct prime factors of 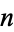 . Then
. Then
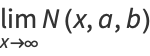 |
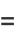 |
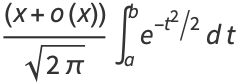 |
(2) |
 |
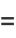 |
![((x+o(x)))/2[erf(b/(sqrt(2)))-erf(a/(sqrt(2)))],](https://mathworld.wolfram.com/images/equations/Erdos-KacTheorem/Inline10.gif) |
(3) |
where 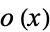 is a Landau symbol.
is a Landau symbol.
The theorem is discussed in Kac (1959).
REFERENCES:
Kac, M. Statistical Independence in Probability, Analysis and Number Theory. New York: Wiley, 1959.
Riesel, H. "The Erdős-Kac Theorem." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 158-159, 1994.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|