


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-12-2020
Date: 19-8-2020
Date: 17-10-2020
|
Let 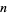 be a positive integer and
be a positive integer and 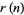 the number of (not necessarily distinct) prime factors of
the number of (not necessarily distinct) prime factors of 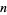 (with
(with 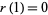 ). Let
). Let 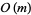 be the number of positive integers
be the number of positive integers 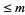 with an odd number of prime factors, and
with an odd number of prime factors, and 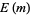 the number of positive integers
the number of positive integers 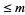 with an even number of prime factors. Pólya (1919) conjectured that
with an even number of prime factors. Pólya (1919) conjectured that
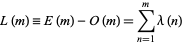 |
is 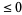 , where
, where 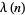 is the Liouville function.
is the Liouville function.
The conjecture was made in 1919, and disproven by Haselgrove (1958) using a method due to Ingham (1942). Lehman (1960) found the first explicit counterexample, 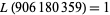 , and the smallest counterexample
, and the smallest counterexample 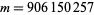 was found by Tanaka (1980). The first
was found by Tanaka (1980). The first 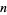 for which
for which 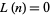 are
are 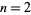 , 4, 6, 10, 16, 26, 40, 96, 586, 906150256, ... (Tanaka 1980, OEIS A028488). It is unknown if
, 4, 6, 10, 16, 26, 40, 96, 586, 906150256, ... (Tanaka 1980, OEIS A028488). It is unknown if 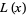 changes sign infinitely often (Tanaka 1980).
changes sign infinitely often (Tanaka 1980).
REFERENCES:
Haselgrove, C. B. "A Disproof of a Conjecture of Pólya." Mathematika 5, 141-145, 1958.
Ingham, A. E. "On Two Conjectures in the Theory of Numbers." Amer. J. Math. 64, 313-319, 1942.
Lehman, R. S. "On Liouville's Function." Math. Comput. 14, 311-320, 1960.
Pólya, G. "Verschiedene Bemerkungen zur Zahlentheorie." Jahresber. deutschen Math.-Verein. 28, 31-40, 1919.
Sloane, N. J. A. Sequence A028488 in "The On-Line Encyclopedia of Integer Sequences."
Tanaka, M. "A Numerical Investigation on Cumulative Sum of the Liouville Function" [sic]. Tokyo J. Math. 3, 187-189, 1980.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|