


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-2-2021
Date: 18-10-2019
Date: 24-1-2021
|
The Feller-Tornier constant is the density of integers that have an even number of prime factors 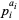 with
with 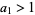 in their prime factorization. It is given by
in their prime factorization. It is given by
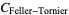 |
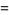 |
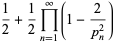 |
(1) |
 |
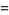 |
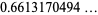 |
(2) |
(OEIS A065493), where 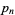 is the
is the 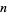 th prime. It can be given by the sum
th prime. It can be given by the sum
![C_(Feller-Tornier)=1/2{1+exp[-sum_(n=1)^infty(2^nP(n))/n]},](https://mathworld.wolfram.com/images/equations/Feller-TornierConstant/NumberedEquation1.gif) |
(3) |
where 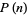 is the prime zeta function.
is the prime zeta function.
REFERENCES:
Cohen, E. "Some Asymptotic Formulas in the Theory of Numbers." Trans. Amer. Math. Soc. 112, 214-227, 1964.
Feller, W. and Tornier, E. "Mengentheoretische Untersuchungen von Eigenschaften der Zahlenreihe." Math. Ann. 107, 188-232, 1933.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 106, 2003.
Niklasch, G. "Some Number-Theoretical Constants." https://www.gn-50uma.de/alula/essays/Moree/Moree.en.shtml.
Schoenberg, I. J. "On Asymptotic Distributions of Arithmetical Functions." Trans. Amer. Math. Soc. 39, 315-330, 1936.
Sloane, N. J. A. Sequence A065493 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|