


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-9-2020
Date: 5-6-2020
Date: 13-2-2020
|
Given an integer  , the Payam number
, the Payam number  is the smallest positive odd integer
is the smallest positive odd integer  such that for every positive integer
such that for every positive integer  , the number
, the number  is not divisible by any primes
is not divisible by any primes  such that the multiplicative order of 2
such that the multiplicative order of 2  is less than or equal to
is less than or equal to  . Payam numbers are good candidates for searching for Proth primes, i.e., primes of the form
. Payam numbers are good candidates for searching for Proth primes, i.e., primes of the form 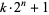 , as well as primes of the form
, as well as primes of the form 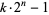 .
.
The first few values of 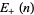 for
for 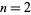 , 3, ... are 3, 9, 15, 105, 105, 105, 105, 105, 165, 165, 75075, ... (OEIS A083556), and the first few values of
, 3, ... are 3, 9, 15, 105, 105, 105, 105, 105, 165, 165, 75075, ... (OEIS A083556), and the first few values of 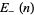 are 3, 3, 45, 45, 45, 45, 45, 45, 45, 2145, ... (OEIS A083391).
are 3, 3, 45, 45, 45, 45, 45, 45, 45, 2145, ... (OEIS A083391).
REFERENCES:
Sloane, N. J. A. Sequences A083391 and A083556 in "The On-Line Encyclopedia of Integer Sequences."
Smith, R. "A Co-Ordinated Search for Primes in the Payam Number Series." https://home.btclick.com/rwsmith/pp/payam3.htm.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|