


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-10-2020
Date: 9-12-2020
Date: 20-7-2020
|
Euler's 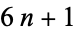 theorem states that every prime of the form
theorem states that every prime of the form 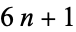 , (i.e., 7, 13, 19, 31, 37, 43, 61, 67, ..., which are also the primes of the form
, (i.e., 7, 13, 19, 31, 37, 43, 61, 67, ..., which are also the primes of the form 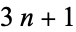 ; OEIS A002476) can be written in the form
; OEIS A002476) can be written in the form  with
with  and
and  positive integers.
positive integers.
The first few positive integers that can be represented in this form (with 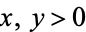 ) are 4, 7, 12, 13, 16, 19, ... (OEIS A092572), summarized in the following table together with their representations.
) are 4, 7, 12, 13, 16, 19, ... (OEIS A092572), summarized in the following table together with their representations.
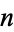 |
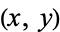 |
| 4 | (1, 1) |
| 7 | (2, 1) |
| 12 | (3, 1) |
| 13 | (1, 2) |
| 16 | (2, 2) |
| 19 | (4, 1) |
| 21 | (3, 2) |
| 28 | (1, 3), (4, 2), (5, 1) |
| 31 | (2, 3) |
Restricting solutions such that 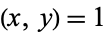 (i.e.,
(i.e., 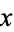 and
and 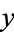 are relatively prime), the numbers that can be represented as
are relatively prime), the numbers that can be represented as 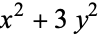 are 4, 7, 12, 13, 19, 21, 28, 31, 37, 39, 43, ... (OEIS A092574), as summarized in the following table.
are 4, 7, 12, 13, 19, 21, 28, 31, 37, 39, 43, ... (OEIS A092574), as summarized in the following table.
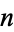 |
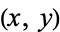 with with 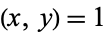 |
| 4 | (1, 1) |
| 7 | (2, 1) |
| 12 | (3, 1) |
| 13 | (1, 2) |
| 19 | (4, 1) |
| 21 | (3, 2) |
| 28 | (1, 3), (5, 1) |
| 31 | (2, 3) |
| 37 | (5, 2) |
REFERENCES:
Sloane, N. J. A. Sequences A002476/M4344, A092572, A092573, A092574, and A092575 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|