


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-8-2020
Date: 8-11-2020
Date: 14-1-2020
|
Like the entire harmonic series, the harmonic series
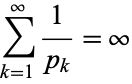 |
(1) |
taken over all primes 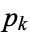 also diverges, as first shown by Euler in 1737 (Nagell 1951, p. 59; Hardy and Wright 1979, pp. 17 and 22; Wells 1986, p. 41; Havil 2003, pp. 28-31), although it does so very slowly. The sum exceeds 1, 2, 3, ... after 3, 59, 361139, ... (OEIS A046024) primes.
also diverges, as first shown by Euler in 1737 (Nagell 1951, p. 59; Hardy and Wright 1979, pp. 17 and 22; Wells 1986, p. 41; Havil 2003, pp. 28-31), although it does so very slowly. The sum exceeds 1, 2, 3, ... after 3, 59, 361139, ... (OEIS A046024) primes.
Its asymptotic behavior is given by
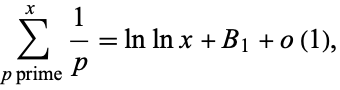 |
(2) |
where
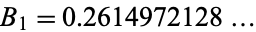 |
(3) |
(OEIS A077761) is the Mertens constant (Hardy and Wright 1979, p. 351; Hardy 1999, p. 50; Havil 2003, p. 64).
REFERENCES:
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. "Prime Numbers" and "The Sequence of Primes." §1.2 and 1.4 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 1-4, 17, 22, and 251, 1979.
Havil, J. "Harmonic Series of Primes." §3.2 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 28-31, 2003.
Nagell, T. Introduction to Number Theory. New York: Wiley, 1951.
Sloane, N. J. A. Sequences A046024 and A077761 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 41, 1986.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|