


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-3-2020
Date: 24-11-2020
Date: 17-1-2021
|
If two numbers  and
and  have the property that their difference
have the property that their difference  is integrally divisible by a number
is integrally divisible by a number  (i.e.,
(i.e.,  is an integer), then
is an integer), then  and
and  are said to be "congruent modulo
are said to be "congruent modulo  ." The number
." The number  is called the modulus, and the statement "
is called the modulus, and the statement " is congruent to
is congruent to  (modulo
(modulo  )" is written mathematically as
)" is written mathematically as
 |
(1) |
If  is not integrally divisible by
is not integrally divisible by  , then it is said that "
, then it is said that " is not congruent to
is not congruent to  (modulo
(modulo  )," which is written
)," which is written
 |
(2) |
The explicit "(mod  )" is sometimes omitted when the modulus
)" is sometimes omitted when the modulus  is understood by context, so in such cases, care must be taken not to confuse the symbol
is understood by context, so in such cases, care must be taken not to confuse the symbol  with the equivalence sign.
with the equivalence sign.
The quantity  is sometimes called the "base," and the quantity
is sometimes called the "base," and the quantity  is called the residue or remainder. There are several types of residues. The common residue defined to be nonnegative and smaller than
is called the residue or remainder. There are several types of residues. The common residue defined to be nonnegative and smaller than  , while the minimal residue is
, while the minimal residue is  or
or  , whichever is smaller in absolute value.
, whichever is smaller in absolute value.

Congruence arithmetic is perhaps most familiar as a generalization of the arithmetic of the clock. Since there are 60 minutes in an hour, "minute arithmetic" uses a modulus of  . If one starts at 40 minutes past the hour and then waits another 35 minutes,
. If one starts at 40 minutes past the hour and then waits another 35 minutes,  , so the current time would be 15 minutes past the (next) hour.
, so the current time would be 15 minutes past the (next) hour.
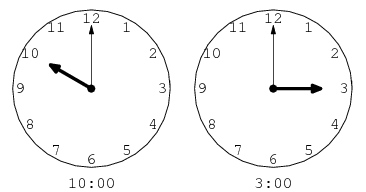
Similarly, "hour arithmetic" on a 12-hour clock uses a modulus of  , so 10 o'clock (a.m.) plus five hours gives
, so 10 o'clock (a.m.) plus five hours gives  , or 3 o'clock (p.m.)
, or 3 o'clock (p.m.)
Congruences satisfy a number of important properties, and are extremely useful in many areas of number theory. Using congruences, simple divisibility tests to check whether a given number is divisible by another number can sometimes be derived. For example, if the sum of a number's digits is divisible by 3 (9), then the original number is divisible by 3 (9).
Congruences also have their limitations. For example, if  and
and  , then it follows that
, then it follows that  , but usually not that
, but usually not that  or
or  . In addition, by "rolling over," congruences discard absolute information. For example, knowing the number of minutes past the hour is useful, but knowing the hour the minutes are past is often more useful still.
. In addition, by "rolling over," congruences discard absolute information. For example, knowing the number of minutes past the hour is useful, but knowing the hour the minutes are past is often more useful still.
Let  and
and  , then important properties of congruences include the following, where
, then important properties of congruences include the following, where  means "implies":
means "implies":
1. Equivalence:  (which can be regarded as a definition).
(which can be regarded as a definition).
2. Determination: either  or
or  .
.
3. Reflexivity:  .
.
4. Symmetry:  .
.
5. Transitivity:  and
and  .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11.  and
and ![a=b (mod m_2)=>a=b (mod [m_1,m_2])](https://mathworld.wolfram.com/images/equations/Congruence/Inline51.gif) , where
, where ![[m_1,m_2]](https://mathworld.wolfram.com/images/equations/Congruence/Inline52.gif) is the least common multiple.
is the least common multiple.
12.  , where
, where  is the greatest common divisor.
is the greatest common divisor.
13. If  , then
, then  , for
, for  a polynomial.
a polynomial.
Properties (6-8) can be proved simply by defining
 |
 |
 |
(3) |
 |
 |
 |
(4) |
where  and
and  are integers. Then
are integers. Then
 |
 |
 |
(5) |
 |
 |
 |
(6) |
 |
 |
 |
(7) |
so the properties are true.
Congruences also apply to fractions. For example, note that
 |
(8) |
so
 |
(9) |
To find  (mod
(mod  ) where
) where  (i.e.,
(i.e.,  and
and  are relatively prime), use an algorithm similar to the greedy algorithm. Let
are relatively prime), use an algorithm similar to the greedy algorithm. Let  and find
and find
![p_0=[m/(q_0)],](https://mathworld.wolfram.com/images/equations/Congruence/NumberedEquation5.gif) |
(10) |
where ![[x]](https://mathworld.wolfram.com/images/equations/Congruence/Inline81.gif) is the ceiling function, then compute
is the ceiling function, then compute
 |
(11) |
Iterate until  , then
, then
 |
(12) |
This method always works for  prime, and sometimes even for
prime, and sometimes even for  composite. However, for a composite
composite. However, for a composite  , the method can fail by reaching 0 (Conway and Guy 1996).
, the method can fail by reaching 0 (Conway and Guy 1996).
Finding a fractional congruence is equivalent to solving a corresponding linear congruence equation
 |
(13) |
A fractional congruence of a unit fraction is known as a modular inverse. A fractional congruence can be found in the Wolfram Language using the following function:
FractionalMod[r_Rational, m_Integer] := Mod[
Numerator[r]PowerMod[Denominator[r], -1, m], m]
or using the undocumented syntax PolynomialMod[r, m] for  an explicit rational number.
an explicit rational number.
REFERENCES:
Burton, D. M. "The Theory of Congruences." Ch. 4 in Elementary Number Theory, 4th ed. Boston, MA: Allyn and Bacon, pp. 80-105, 1989.
Conway, J. H. and Guy, R. K. "Arithmetic Modulo  ." In The Book of Numbers. New York: Springer-Verlag, pp. 130-132, 1996.
." In The Book of Numbers. New York: Springer-Verlag, pp. 130-132, 1996.
Courant, R. and Robbins, H. "Congruences." §2 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 31-40, 1996.
Hardy, G. H. and Wright, E. M. "Congruences and Classes of Residues," "Elementary Properties of Congruences," "Linear Congruences," "General Properties of Congruences," and "Congruences to Composite Moduli." §5.2-5.4 and Chs. 7-8 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 49-52 and 82-106, 1979.
Hilton, P.; Holton, D.; and Pedersen, J. "A Far Nicer Arithmetic." Ch. 2 in Mathematical Reflections in a Room with Many Mirrors. New York: Springer-Verlag, pp. 25-60, 1997.
Jones, G. A. and Jones, J. M. "Congruences." Ch. 3 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 37-63, 1998.
Nagell, T. "Theory of Congruences." Ch. 3 in Introduction to Number Theory. New York: Wiley, pp. 68-131, 1951.
Séroul, R. "Congruences." §2.5 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 11-12, 2000.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 55, 1993.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|