Signature Sequence

Let 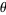 be an irrational number, define 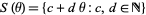, and let  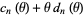be the sequence obtained by arranging the elements of  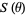in increasing order. A sequence  is said to be a signature sequence if there exists a positive irrational number 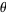 such that 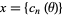, and  is called the signature of .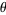

One can also define two extended signature sequences for positive rational 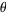 by taking the  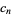in increasing order or decreasing order. These can be considered signature sequences for  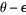and 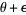, respectively, where  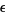is an infinitesimal.

The signature of an irrational number or either signature of a rational number is a fractal sequence. Also, if  is a signature or extended signature sequence, then the lower-trimmed subsequence is 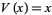. It has been conjectured that every sequence with both of these properties is a signature or extended signature sequence.

If every initial subsequence of a sequence 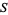 is an initial subsequence of some signature sequence, then  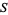is either a signature sequence, an extended signature sequence, or one of the two limiting cases: all 1's, or the natural numbers (which could be regarded as signature sequences for zero and infinity).

REFERENCES:

Kimberling, C. "Fractal Sequences and Interspersions." Ars Combin. 45, 157-168, 1997.