
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-9-2020
Date: 11-8-2020
Date: 2-1-2020
|

Stern's diatomic series is the sequence
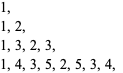 |
(1) |
... (OEIS A002487) which arises in the Calkin-Wilf tree. It is sometimes also known as the fusc function (Dijkstra 1982).
The 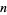 th term can be given by the recurrence equation
th term can be given by the recurrence equation
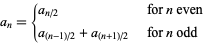 |
(2) |
with 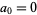 and
and  . A sum formula is given by
. A sum formula is given by
 |
(3) |
A generating function is given by
 |
 |
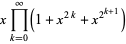 |
(4) |
 |
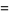 |
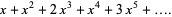 |
(5) |
REFERENCES:
Calkin, N. and Wilf, H. S. "Recounting the Rationals." Amer. Math. Monthly 107, 360-363, 2000.
Dijkstra, E. W. Selected Writings on Computing: A Personal Perspective. New York: Springer-Verlag, pp. 215-232, 1982.
Gibbons, L.; Lester, D.; and Bird, R. "Functional Pearl: Enumerating the Rationals." J. Func. Prog. 16, 281-291, 2006.
Sloane, N. J. A. Sequence A002487/M0141 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|