


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-7-2020
Date: 8-5-2020
Date: 26-8-2020
|
A "weird number" is a number that is abundant (i.e., the sum of proper divisors is greater than the number) without being pseudoperfect (i.e., no subset of the proper divisors sums to the number itself). The pseudoperfect part of the definition means that finding weird numbers is a case of the subset sum problem.
Since prime numbers are deficient, prime numbers are not weird. Similarly, since multiples of 6 are pseudoperfect, no weird number is a multiple of 6.
The smallest weird number is 70, which has proper divisors 1, 2, 5, 7, 10, 14, and 35. These sum to 74, which is greater that the number itself, so 70 is abundant, and no subset of them sums to 70. In contrast, the smallest abundant number is 12, which has proper divisors 1, 2, 3, 4, and 6. These sum to 16, so 12 is abundant, but the subset sum 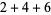 equals 12, so 12 is not weird.
equals 12, so 12 is not weird.
The first few weird numbers are 70, 836, 4030, 5830, 7192, 7912, 9272, 10430, ... (OEIS A006037).
An infinite number of weird numbers are known to exist, and the sequence of weird numbers has positive Schnirelmann density.
No odd weird numbers are known. W. Fang (Sep. 4, 2013) showed there are no odd weird numbers less than 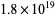 (Sloane).
(Sloane).
Kravitz (1976) showed that for 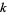 a positive integer and
a positive integer and 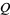 prime, if
prime, if
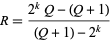 |
(1) |
is prime, then
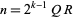 |
(2) |
is a weird number. Kravitz used this result with 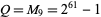 (where
(where 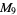 is a Mersenne prime) and
is a Mersenne prime) and 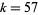 to obtain the 53-digit weird number
to obtain the 53-digit weird number
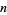 |
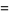 |
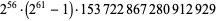 |
(3) |
 |
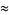 |
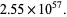 |
(4) |
Other large weird numbers can sometimes be generated using Kravitz's result by starting with a known large prime number 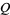 and checking
and checking 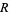 for incremental values of
for incremental values of 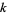 until a prime
until a prime 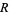 results. For example, taking
results. For example, taking 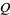 as the Mersenne primes
as the Mersenne primes 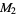 ,
, 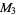 , ..., the first few indices
, ..., the first few indices 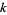 giving prime
giving prime 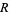 are 2, 4, 4, 11, 13, 16, 16, 57, and 78, and the numbers of digits in the resulting weird numbers are 2, 4, 5, 11, 13, 16, 19, 53, and 74 (E. Weisstein, Dec. 7, 2013).
are 2, 4, 4, 11, 13, 16, 16, 57, and 78, and the numbers of digits in the resulting weird numbers are 2, 4, 5, 11, 13, 16, 19, 53, and 74 (E. Weisstein, Dec. 7, 2013).
Students from Central Washington University used Kravitz's approach to construct larger weird numbers, the largest having 127 digits (KIMA staff 2013).
REFERENCES:
Benkoski, S. "Are All Weird Numbers Even?" Amer. Math. Monthly 79, 774, 1972.
Benkoski, S. J. and Erdős, P. "On Weird and Pseudoperfect Numbers." Math. Comput. 28, 617-623, 1974.
Guy, R. K. "Almost Perfect, Quasi-Perfect, Pseudoperfect, Harmonic, Weird, Multiperfect and Hyperperfect Numbers." §B2 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 45-53, 1994.
KIMA staff. "CWU: Math Students Break World Record for 'Weird Number."' Dec. 4, 2013. https://www.kimatv.com/news/local/CWU-math-students-234496131.html.
Kravitz, S. "Corrigendum: 'On Weird and Pseudoperfect Numbers."' Math. Comput. 29, 673, 1975.
Kravitz, S. "A Search for Large Weird Numbers." J. Recr. Math. 9, 82-85, 1976.
Sloane, N. J. A. Sequence A006037/M5339 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|