


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-1-2021
Date: 14-8-2020
Date: 16-9-2020
|
A number which is simultaneously a pentagonal number 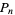 and a square number
and a square number 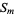 . Such numbers exist when
. Such numbers exist when
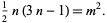 |
(1) |
Completing the square gives
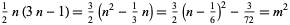 |
(2) |
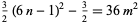 |
(3) |
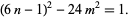 |
(4) |
Substituting 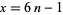 and
and 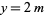 gives the Pell equation
gives the Pell equation
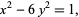 |
(5) |
which has solutions 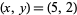 , (49, 20), (485, 198), .... In terms of
, (49, 20), (485, 198), .... In terms of 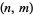 , these give (1,1), (25/3, 10), (81, 99), (2401/3, 980), (7921, 9701), ..., of which the whole number solutions are
, these give (1,1), (25/3, 10), (81, 99), (2401/3, 980), (7921, 9701), ..., of which the whole number solutions are 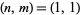 , (81, 99), (7921, 9701), (776161, 950599), ... (OEIS A046172 and A046173), corresponding to the pentagonal square numbers 1, 9801, 94109401, 903638458801, 8676736387298001, ... (OEIS A036353).
, (81, 99), (7921, 9701), (776161, 950599), ... (OEIS A046172 and A046173), corresponding to the pentagonal square numbers 1, 9801, 94109401, 903638458801, 8676736387298001, ... (OEIS A036353).
REFERENCES:
Silverman, J. H. A Friendly Introduction to Number Theory. Englewood Cliffs, NJ: Prentice Hall, 1996.
Sloane, N. J. A. Sequences A036353, A046172, and A046173 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|