Bernoulli Number
The Bernoulli numbers  are a sequence of signed rational numbers that can be defined by the exponential generating function
are a sequence of signed rational numbers that can be defined by the exponential generating function
 |
(1)
|
These numbers arise in the series expansions of trigonometric functions, and are extremely important in number theory and analysis.
There are actually two definitions for the Bernoulli numbers. To distinguish them, the Bernoulli numbers as defined in modern usage (National Institute of Standards and Technology convention) are written 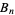 , while the Bernoulli numbers encountered in older literature are written
, while the Bernoulli numbers encountered in older literature are written 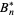 (Gradshteyn and Ryzhik 2000). In each case, the Bernoulli numbers are a special case of the Bernoulli polynomials
(Gradshteyn and Ryzhik 2000). In each case, the Bernoulli numbers are a special case of the Bernoulli polynomials 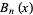 or
or 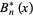 with
with 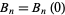 and
and 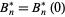 .
.
The Bernoulli number and polynomial should not be confused with the Bell numbers and Bell polynomial, which are also commonly denoted 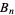 and
and 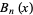 , respectively.
, respectively.
Bernoulli numbers defined by the modern definition are denoted 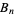 and sometimes called "even-index" Bernoulli numbers. These are the Bernoulli numbers returned, by example, by the Wolfram Language function BernoulliB[n].
and sometimes called "even-index" Bernoulli numbers. These are the Bernoulli numbers returned, by example, by the Wolfram Language function BernoulliB[n].
The Bernoulli number 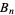 can be defined by the contour integral
can be defined by the contour integral
 |
(2)
|
where the contour encloses the origin, has radius less than 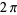 (to avoid the poles at
(to avoid the poles at 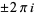 ), and is traversed in a counterclockwise direction (Arfken 1985, p. 413).
), and is traversed in a counterclockwise direction (Arfken 1985, p. 413).
The first few Bernoulli numbers  are
are
(OEIS A000367 and A002445), with
 |
(16)
|
for 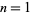 , 2, ....
, 2, ....
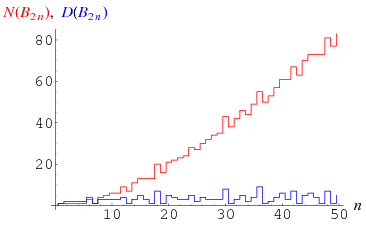
The numbers of digits in the numerator of 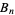 for the
for the 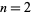 , 4, ... are 1, 1, 1, 1, 1, 3, 1, 4, 5, 6, 6, 9, 7, 11, ... (OEIS A068399), while the numbers of digits in the corresponding denominators are 1, 2, 2, 2, 2, 4, 1, 3, 3, 3, 3, 4, 1, 3, 5, 3, ... (OEIS A092904). Both are plotted above.
, 4, ... are 1, 1, 1, 1, 1, 3, 1, 4, 5, 6, 6, 9, 7, 11, ... (OEIS A068399), while the numbers of digits in the corresponding denominators are 1, 2, 2, 2, 2, 4, 1, 3, 3, 3, 3, 4, 1, 3, 5, 3, ... (OEIS A092904). Both are plotted above.
The denominator of 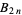 is given by
is given by
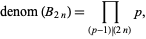 |
(17)
|
where the product is taken over the primes 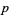 (Ex. 6.54 in Graham et al. 1994), a result which is related to the von Staudt-Clausen theorem.
(Ex. 6.54 in Graham et al. 1994), a result which is related to the von Staudt-Clausen theorem.
The number of digits in the numerators of 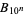 for
for 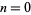 , 1, ... are 1, 1, 83, 1779, 27691, 376772, 4767554, 57675292, 676752609, 7767525702, ... (OEIS A103233), while the corresponding numbers of digits in the denominator are 1, 2, 5, 9, 13, 16, 24, ... (OEIS A114471). The values of the denominators of
, 1, ... are 1, 1, 83, 1779, 27691, 376772, 4767554, 57675292, 676752609, 7767525702, ... (OEIS A103233), while the corresponding numbers of digits in the denominator are 1, 2, 5, 9, 13, 16, 24, ... (OEIS A114471). The values of the denominators of 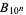 for
for 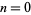 , 1, ... are 66, 33330, 342999030, 2338224387510, 9355235774427510, ... (OEIS A139822).
, 1, ... are 66, 33330, 342999030, 2338224387510, 9355235774427510, ... (OEIS A139822).
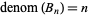 for 1806, but for no other
for 1806, but for no other 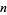 (Kellner 2005).
(Kellner 2005).
The running maxima of denominators are 1, 6, 30, 42, 66, 2730, 14322, 1919190, ... (OEIS A100194), which occur for 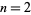 , 4, 6, 8, 12, 14, 32, 38, ... (OEIS A100195).
, 4, 6, 8, 12, 14, 32, 38, ... (OEIS A100195).
The fraction of 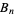 with even
with even 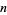 that have denominator 6 is strictly positive (Jensen 1915), with similar results for other denominators (Erdős and Wagstaff 1980, Moreno and Wagstaff 2005).
that have denominator 6 is strictly positive (Jensen 1915), with similar results for other denominators (Erdős and Wagstaff 1980, Moreno and Wagstaff 2005).
Interestingly, a higher proportion of Bernoulli denominators equal 6 than any other value (Sunseri 1980), and the fraction of even Bernoulli numbers with denominator 6 is close to 1/6 (Erdős and Wagstaff 1980). S. Plouffe (pers. comm., Feb. 12, 2007) computed the fraction of even Bernoulli numbers with denominator 6 up to 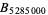 and found it to be 0.1526... and still slowly decreasing.
and found it to be 0.1526... and still slowly decreasing.
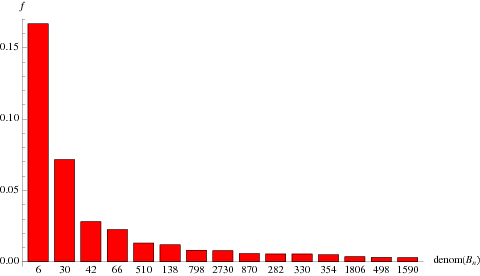
The numbers of Bernoulli numbers less than or equal to 1, 10, 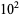 , ... having denominator 6 are 0, 1, 10, 87, 834, ... (OEIS A114648), which approaches the decimal expansion of
, ... having denominator 6 are 0, 1, 10, 87, 834, ... (OEIS A114648), which approaches the decimal expansion of 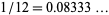 . The above histogram shows the fraction of denominators having given denominators for index up to
. The above histogram shows the fraction of denominators having given denominators for index up to 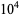 . Ranked in order of frequency, the first few denominators appear to be 6, 30, 42, 66, 510, ... (OEIS A114649).
. Ranked in order of frequency, the first few denominators appear to be 6, 30, 42, 66, 510, ... (OEIS A114649).
The only known Bernoulli numbers 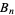 having prime numerators occur for
having prime numerators occur for 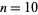 , 12, 14, 16, 18, 36, and 42 (OEIS A092132), corresponding to 5,
, 12, 14, 16, 18, 36, and 42 (OEIS A092132), corresponding to 5, 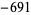 , 7,
, 7, 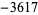 , 43867,
, 43867, 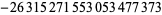 , and 1520097643918070802691 (OEIS A092133), with no other primes for
, and 1520097643918070802691 (OEIS A092133), with no other primes for 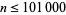 (E. W. Weisstein, Feb. 27, 2007). Wagstaff maintains a page of factorizations of Bernoulli number numerators.
(E. W. Weisstein, Feb. 27, 2007). Wagstaff maintains a page of factorizations of Bernoulli number numerators.
The following table summarizes record computations of the 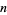 th Bernoulli number
th Bernoulli number 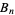 , including giving the number of digits in the numerator.
, including giving the number of digits in the numerator.
 |
digits in numerator |
denominator |
date |
reference |
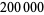 |
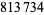 |
14977732474858443510 |
|
Fee and Plouffe |
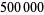 |
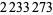 |
584711591137493802510 |
2002 |
Plouffe (2002) |
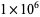 |
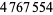 |
936123257411127577818510 |
Dec. 16, 2002 |
Kellner |
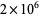 |
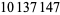 |
9601480183016524970884020224910 |
Feb. 10, 2003 |
Kellner |
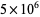 |
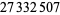 |
936123257411127577818510 |
Oct. 8, 2005 |
O. Pavlyk (pers. comm.) |
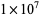 |
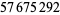 |
9601480183016524970884020224910 |
Feb. 2008 |
O. Pavlyk (2008) |
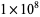 |
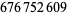 |
394815332706046542049668428841497001870 |
Oct. 2008 |
D. Harvey (2008) |
The denominator of 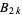 (mod 1) is given by the von Staudt-Clausen theorem, which also implies that the denominator of
(mod 1) is given by the von Staudt-Clausen theorem, which also implies that the denominator of 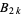 is squarefree (Hardy and Wright 1979). Another curious property is that the fractional part of
is squarefree (Hardy and Wright 1979). Another curious property is that the fractional part of 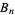 has a decimal expansion period that divides
has a decimal expansion period that divides 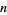 , and there is a single digit before that period (Conway 1996). In particular, the periods of
, and there is a single digit before that period (Conway 1996). In particular, the periods of 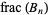 for
for 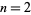 , 4, ... are 1, 1, 6, 1, 2, 6, 1, 16, 18, 2, 22, ... (OEIS A112828), and the corresponding values of
, 4, ... are 1, 1, 6, 1, 2, 6, 1, 16, 18, 2, 22, ... (OEIS A112828), and the corresponding values of 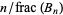 are 2, 4, 1, 8, 5, 2, 14, 1, 1, 10, ... (OEIS A112829).
are 2, 4, 1, 8, 5, 2, 14, 1, 1, 10, ... (OEIS A112829).
Consider the generating function
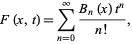 |
(18)
|
which converges uniformly for 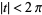 and all
and all  (Castellanos 1988). Taking the partial derivative gives
(Castellanos 1988). Taking the partial derivative gives
The solution to this differential equation can be found using separation of variables as
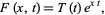 |
(22)
|
so integrating gives
But integrating (24) explicitly gives
so
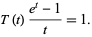 |
(28)
|
Solving for 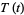 and plugging back into (◇) then gives
and plugging back into (◇) then gives
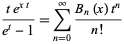 |
(29)
|
(Castellanos 1988). Setting 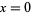 and adding
and adding 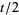 to both sides then gives
to both sides then gives
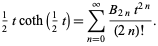 |
(30)
|
Letting 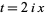 then gives
then gives
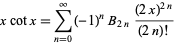 |
(31)
|
for ![x in [-pi,pi]](https://mathworld.wolfram.com/images/equations/BernoulliNumber/Inline132.gif) .
.
The Bernoulli numbers may also be calculated from
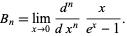 |
(32)
|
The Bernoulli numbers are given by the double sum
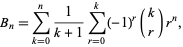 |
(33)
|
where 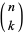 is a binomial coefficient. They also satisfy the sum
is a binomial coefficient. They also satisfy the sum
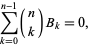 |
(34)
|
which can be solved for 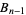 to give a recurrence relation for computing
to give a recurrence relation for computing 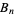 . By adding
. By adding 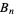 to both sides of (34), it can be written simply as
to both sides of (34), it can be written simply as
![(B+1)^([n])=B^([n]),](https://mathworld.wolfram.com/images/equations/BernoulliNumber/NumberedEquation14.gif) |
(35)
|
where the notation ![B^([k])](https://mathworld.wolfram.com/images/equations/BernoulliNumber/Inline137.gif) means the quantity in question is raised to the appropriate power
means the quantity in question is raised to the appropriate power 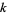 and all terms of the form
and all terms of the form 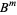 are replaced with the corresponding Bernoulli numbers
are replaced with the corresponding Bernoulli numbers 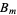 .
.
as well as the interesting sums
(Lehmer 1935, Carlitz 1968, Štofka 2014), as well as the nice sum identity
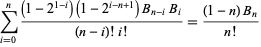 |
(39)
|
(Gosper).
An asymptotic series for the even Bernoulli numbers is
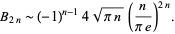 |
(40)
|
Bernoulli numbers appear in expressions of the form 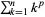 , where
, where 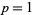 , 2, .... Bernoulli numbers also appear in the series expansions of functions involving
, 2, .... Bernoulli numbers also appear in the series expansions of functions involving 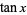 ,
, 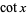 ,
, 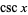 ,
, 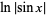 ,
, 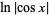 ,
, 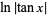 ,
, 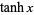 ,
, 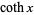 , and
, and 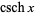 .
.
An analytic solution exists for even orders,
for 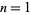 , 2, ..., where
, 2, ..., where 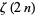 is the Riemann zeta function. Another intimate connection with the Riemann zeta function is provided by the identity
is the Riemann zeta function. Another intimate connection with the Riemann zeta function is provided by the identity
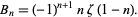 |
(43)
|
An integral in terms of the Euler polynomial is given by
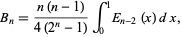 |
(44)
|
where 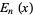 is an Euler polynomial (J. Crepps, pers. comm., Apr. 2002).
is an Euler polynomial (J. Crepps, pers. comm., Apr. 2002).
Bernoulli first used the Bernoulli numbers while computing 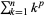 . He used the property of the figurate number triangle that
. He used the property of the figurate number triangle that
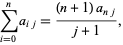 |
(45)
|
along with a form for 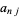 which he derived inductively to compute the sums up to
which he derived inductively to compute the sums up to 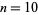 (Boyer 1968, p. 85). For
(Boyer 1968, p. 85). For 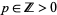 , the sum is given by
, the sum is given by
![sum_(k=1)^nk^p=((B+n+1)^([p+1])-B^([p+1]))/(p+1),](https://mathworld.wolfram.com/images/equations/BernoulliNumber/NumberedEquation20.gif) |
(46)
|
where again the notation ![B^([k])](https://mathworld.wolfram.com/images/equations/BernoulliNumber/Inline174.gif) means the quantity in question is raised to the appropriate power
means the quantity in question is raised to the appropriate power 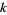 and all terms of the form
and all terms of the form 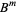 are replaced with the corresponding Bernoulli numbers
are replaced with the corresponding Bernoulli numbers 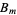 . Note that it is common (e.g., Carlitz 1965) to simply write
. Note that it is common (e.g., Carlitz 1965) to simply write 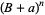 with the understanding that after expansion,
with the understanding that after expansion, 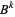 is replaced by
is replaced by 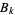 .
.
Written explicitly in terms of a sum of powers,
where
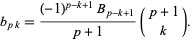 |
(50)
|
Taking 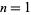 gives Bernoulli's observation that the coefficients of the terms
gives Bernoulli's observation that the coefficients of the terms 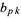 sum to 1,
sum to 1,
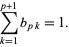 |
(51)
|
Ramanujan gave a number of curious infinite sum identities involving Bernoulli numbers (Berndt 1994).

Plouffe (pers. comm., Jun. 21, 2004) conjectured that the fractional parts of positive Bernoulli numbers of the form 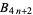 satisfy either
satisfy either 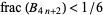 or
or 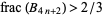 . However, there are many counterexamples, the first few of which occur for
. However, there are many counterexamples, the first few of which occur for 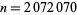 (found by Plouffe also on Jun. 21, 2004), 6216210, 8128890, 10360350, 13548150, ... (OEIS A155125). Interestingly, all of these are numbers having a large number of factors in their primes factorizations, as summarized in the following table. The indices of these numbers having incrementally smallest value of
(found by Plouffe also on Jun. 21, 2004), 6216210, 8128890, 10360350, 13548150, ... (OEIS A155125). Interestingly, all of these are numbers having a large number of factors in their primes factorizations, as summarized in the following table. The indices of these numbers having incrementally smallest value of 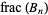 are given by 2072070, 6216210, 10360350, 18648630, 31081050, 35225190, 93243150, ... (OEIS A155126), which appear to tend to occur at positions in the original list that are powers of 2 (1, 2, 4, 8, 16, 18, 64, ...).
are given by 2072070, 6216210, 10360350, 18648630, 31081050, 35225190, 93243150, ... (OEIS A155126), which appear to tend to occur at positions in the original list that are powers of 2 (1, 2, 4, 8, 16, 18, 64, ...).
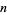 |
factorization of 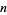 |
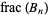 |
| 2072070 |
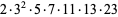 |
0.6664435068 |
| 6216210 |
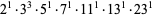 |
0.6588649656 |
| 8128890 |
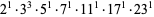 |
0.6648723198 |
| 10360350 |
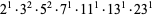 |
0.6564013890 |
The older definition of the Bernoulli numbers, no longer in widespread use, defines 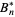 using the equations
using the equations
or
for 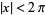 (Whittaker and Watson 1990, p. 125). The
(Whittaker and Watson 1990, p. 125). The 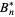 Bernoulli numbers may be calculated from the integral
Bernoulli numbers may be calculated from the integral
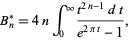 |
(56)
|
and analytically from
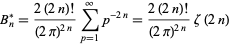 |
(57)
|
for 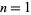 , 2, ..., where
, 2, ..., where 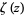 is the Riemann zeta function.
is the Riemann zeta function.
The Bernoulli numbers 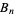 are a superset of the archaic ones
are a superset of the archaic ones 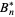 since
since
![B_n=<span style=]() {1 for n=0; -1/2 for n=1; (-1)^((n/2)-1)B_(n/2)^* for n even; 0 for n odd. " src="https://mathworld.wolfram.com/images/equations/BernoulliNumber/NumberedEquation25.gif" style="height:96px; width:196px" /> {1 for n=0; -1/2 for n=1; (-1)^((n/2)-1)B_(n/2)^* for n even; 0 for n odd. " src="https://mathworld.wolfram.com/images/equations/BernoulliNumber/NumberedEquation25.gif" style="height:96px; width:196px" /> |
(58)
|
The first few Bernoulli numbers 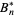 are
are
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula." §23.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 804-806, 1972.
Arfken, G. "Bernoulli Numbers, Euler-Maclaurin Formula." §5.9 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 327-338, 1985.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 71, 1987.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 81-85, 1994.
Boyer, C. B. "Pascal's Formula for the Sums of Powers of the Integers." Scripta Math. 9, 237-244, 1943.
Boyer, C. B. A History of Mathematics. New York: Wiley, 1968.
Carlitz, L. "Bernoulli Numbers." Fib. Quart. 6, 71-85, 1968.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. In The Book of Numbers. New York: Springer-Verlag, pp. 107-110, 1996.
Dilcher, K. and Slavutskii, I. Sh. "A Bibliography of Bernoulli Numbers." http://www.mathstat.dal.ca/~dilcher/bernoulli.html.
Erdős, P. and Wagstaff, S. S. "The Fractional Parts of the Bernoulli Numbers." Illinois J. Math. 24, 104-112, 1980.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Bernoulli Numbers." §6.5 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 283-290, 1994.
Hardy, G. H. and Wright, W. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 91-93, 1979.
Harvey, D. "A Multimodular Algorithm for Computing Bernoulli Numbers." Preprint. Oct. 13, 2008. http://cims.nyu.edu/~harvey/bernmm/bernmm.pdf.
Harvey, D. "A Multimodular Algorithm for Computing Bernoulli Numbers." http://cims.nyu.edu/~harvey/bernmm/.
Hauss, M. Verallgemeinerte Stirling, Bernoulli und Euler Zahlen, deren Anwendungen und schnell konvergente Reihen für Zeta Funktionen. Aachen, Germany: Verlag Shaker, 1995.
Havil, J. "Bernoulli Numbers." §10.1 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 81-84, 2003.
Ireland, K. and Rosen, M. "Bernoulli Numbers." Ch. 15 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 228-248, 1990.
Jensen, K. L. "Om talteoretiske Egenskaber ved de Bernoulliske Tal." Nyt Tidskrift für Math. Afdeling B 28, 73-83, 1915.
Kellner, B. C. "The Bernoulli Number Page." http://www.bernoulli.org/.
Kellner, B. C. "The Equation 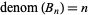 Has Only One Solution." Apr. 2, 2005. http://www.bernoulli.org/~bk/denombneqn.pdf.
Has Only One Solution." Apr. 2, 2005. http://www.bernoulli.org/~bk/denombneqn.pdf.
Knuth, D. E. and Buckholtz, T. J. "Computation of Tangent, Euler, and Bernoulli Numbers." Math. Comput. 21, 663-688, 1967.
Lehmer, D. H. "Lacunary Recurrences for the Bernoulli Numbers." Ann. Math. 36, 637-649, 1935.
Moreno, C. J. and Wagstaff, S. S. §3.9 in Sums of Squares of Integers. Chapman & Hall/CRC, 2005.
Nielsen, N. Traité élémentaire des nombres de Bernoulli. Paris: Gauthier-Villars, 1923.
Oakes, M. "Re: Prime Bernoulli Numerators." primenumbers group. Feb. 11, 2004. http://groups.yahoo.com/group/primenumbers/message/14550.
Pavlyk, O. "Today We Broke the Bernoulli Record: From the Analytical Engine to Mathematica." Wolfram Blog, Apr. 29, 2008. http://blog.wolfram.com/2008/04/29/today-we-broke-the-bernoulli-record-from-the-analytical-engine-to-mathematica/.
Plouffe, S. "Table of Current Records for the Computation of Constants." http://pi.lacim.uqam.ca/eng/records_en.html.
Plouffe, S. "The 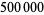 th Bernoulli Number." May 21, 2002. http://www.lacim.uqam.ca/~plouffe/ber500000.txt.
th Bernoulli Number." May 21, 2002. http://www.lacim.uqam.ca/~plouffe/ber500000.txt.
Ramanujan, S. "Some Properties of Bernoulli's Numbers." J. Indian Math. Soc. 3, 219-234, 1911.
Roman, S. The Umbral Calculus. New York: Academic Press, p. 31, 1984.
Sloane, N. J. A. Sequences A000367/M4039, A002445/M4189, A068399, A092132, A092132, A092904, A100194, A100195, A103233, A112828, A112829, A114471 A114648, A114649, A155125, and A155126 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Bernoulli Numbers, 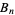 ." Ch. 4 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 35-38, 1987.
." Ch. 4 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 35-38, 1987.
Stein, W. "Computing Bernoulli Numbers." Feb. 16, 2005. http://modular.ucsd.edu/talks/bernoulli/current.pdf.
Štofka, M. Problem 11791. Amer. Math. Monthly 121, 648, 2014.
Sunseri, R. F. Zeros of a 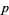 -adic
-adic 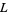 -Functions and Densities Relating to Bernoulli Numbers. Ph.D. thesis. Urbana, IL: University of Illinois at Urbana-Champaign, 1980.
-Functions and Densities Relating to Bernoulli Numbers. Ph.D. thesis. Urbana, IL: University of Illinois at Urbana-Champaign, 1980.
Tanner, J. W. and Wagstaff, S. S. Jr. "New Congruences for the Bernoulli Numbers." Math. Comput. 48, 341-350, 1987.
Wagstaff, S. S. Jr. "Ramanujan's Paper on Bernoulli Numbers." J. Indian Math. Soc. 45, 49-65, 1981.
Wagstaff, S. S. Jr. "bnum." [Factors of absolute values of Bernoulli numerators.] Aug. 17, 2011.http://homes.cerias.purdue.edu/~ssw/bernoulli/bnum.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Woon, S. C. "Generalization of a Relation Between the Riemann Zeta Function and Bernoulli Numbers." 24 Dec 1998. http://arxiv.org/abs/math.NT/9812143.
Young, P. T. "Congruences for Bernoulli, Euler, and Stirling Numbers." J. Number Th. 78, 204-227, 1999.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


