


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-2-2020
Date: 15-3-2020
Date: 14-12-2019
|
The Narayan number 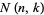 for
for 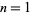 , 2, ... and
, 2, ... and 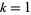 , ...,
, ..., 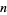 gives a solution to several counting problems in combinatorics. For example,
gives a solution to several counting problems in combinatorics. For example, 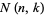 gives the number of expressions with
gives the number of expressions with 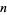 pairs of parentheses that are correctly matched and contain
pairs of parentheses that are correctly matched and contain 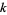 distinct nestings. It also gives the number Dyck paths of length
distinct nestings. It also gives the number Dyck paths of length 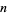 with exactly
with exactly 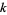 peaks.
peaks.
A closed-form expression of 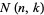 is given by
is given by
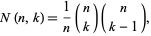 |
where 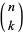 is a binomial coefficient.
is a binomial coefficient.
Summing over 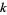 gives the Catalan number
gives the Catalan number
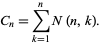 |
Enumerating 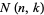 as a number triangle is called the Narayana triangle.
as a number triangle is called the Narayana triangle.
REFERENCES:
MacMahon, P. A. Combinatory Analysis, 2 vols. New York: Chelsea, 1960.
Narayana, T. V. Lattice Path Combinatorics with Statistical Applications. Toronto, Canada: University of Toronto Press, pp. 100-101, 1979.
Stanley, R. P. Problems 6.36(a) and (b) in Enumerative Combinatorics, Vol. 2. Cambridge, England: Cambridge University Press, 1999.



|
|
|
|
دراسة تكشف "مفاجأة" غير سارة تتعلق ببدائل السكر
|
|
|
|
|
|
|
أدوات لا تتركها أبدًا في سيارتك خلال الصيف!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تؤكد الحاجة لفنّ الخطابة في مواجهة تأثيرات الخطابات الإعلامية المعاصرة
|
|
|