


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-1-2021
Date: 7-6-2020
Date: 13-6-2020
|
A prime power is a prime or integer power of a prime. A test for a number 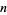 being a prime power will be implemented in the Wolfram Language as PrimePowerQ[n].
being a prime power will be implemented in the Wolfram Language as PrimePowerQ[n].
The first few prime powers are 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 23, 25, ... (OEIS A000961). The first few prime powers with power 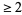 are given by 4, 8, 9, 16, 25, 27, 32, 49, 64, 81, ... (OEIS A025475). The number of prime powers (exponents
are given by 4, 8, 9, 16, 25, 27, 32, 49, 64, 81, ... (OEIS A025475). The number of prime powers (exponents 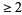 ) up to
) up to  is given by
is given by
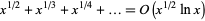 |
(Hardy 1999, p. 27).
The following table gives prime 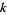 th powers.
th powers.
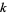 |
OEIS | prime 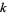 th powers th powers |
| 1 | A000040 | 2, 3, 5, 7, 11, 13, 17, 19, 23, ... |
| 2 | A001248 | 4, 9, 25, 49, 121, 169, 289, 361, ... |
| 3 | A030078 | 8, 27, 125, 343, 1331, 2197, 4913, ... |
| 4 | A030514 | 16, 81, 625, 2401, 14641, 28561, 83521, ... |
| 5 | A050997 | 32, 243, 3125, 16807, 161051, 371293, ... |
REFERENCES:
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Sloane, N. J. A. Sequences A000040/M0652, A000961/M0517, A001248, A025475, A030078, A030514, and A050997 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|