


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-4-2021
Date: 15-3-2021
Date: 20-4-2021
|
Given a formula 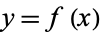 with an absolute error in
with an absolute error in 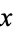 of
of 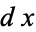 , the absolute error is
, the absolute error is 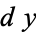 . The relative error is
. The relative error is 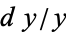 . If
. If 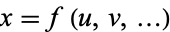 , then
, then
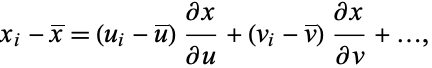 |
(1) |
where 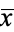 denotes the mean, so the sample variance is given by
denotes the mean, so the sample variance is given by
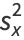 |
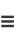 |
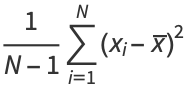 |
(2) |
 |
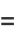 |
![1/(N-1)sum_(i=1)^(N)[(u_i-u^_)^2((partialx)/(partialu))^2+(v_i-v^_)^2((partialx)/(partialv))^2+2(u_i-u^_)(v_i-v^_)((partialx)/(partialu))((partialx)/(partialv))+...].](https://mathworld.wolfram.com/images/equations/ErrorPropagation/Inline13.gif) |
(3) |
The definitions of variance and covariance then give
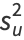 |
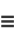 |
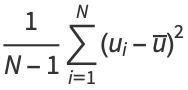 |
(4) |
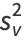 |
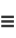 |
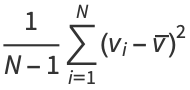 |
(5) |
 |
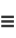 |
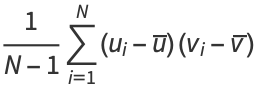 |
(6) |
(where 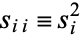 ), so
), so
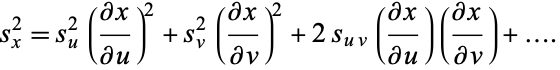 |
(7) |
If 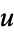 and
and 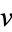 are uncorrelated, then
are uncorrelated, then 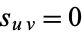 so
so
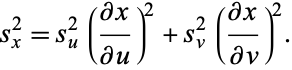 |
(8) |
Now consider addition of quantities with errors. For 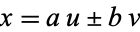 ,
, 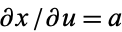 and
and 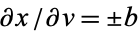 , so
, so
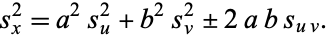 |
(9) |
For division of quantities with 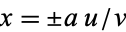 ,
, 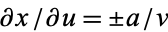 and
and 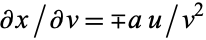 , so
, so
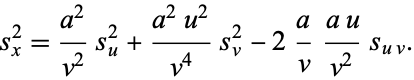 |
(10) |
Dividing through by 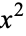 and rearranging then gives
and rearranging then gives
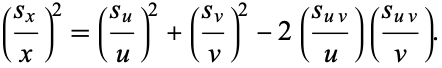 |
(11) |
For exponentiation of quantities with
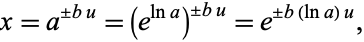 |
(12) |
and
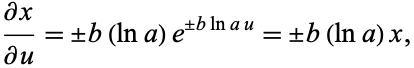 |
(13) |
so
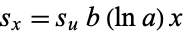 |
(14) |
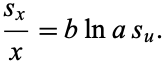 |
(15) |
If 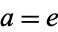 , then
, then
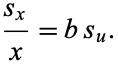 |
(16) |
For logarithms of quantities with 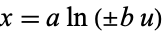 ,
, 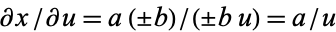 , so
, so
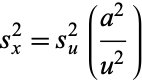 |
(17) |
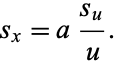 |
(18) |
For multiplication with 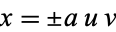 ,
, 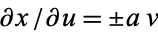 and
and 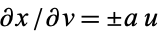 , so
, so
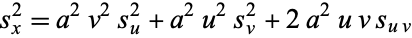 |
(19) |
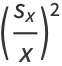 |
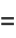 |
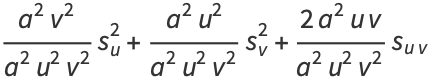 |
(20) |
 |
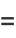 |
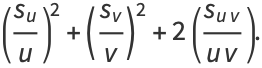 |
(21) |
For powers, with 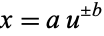 ,
, 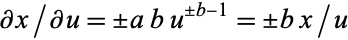 , so
, so
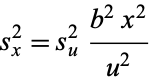 |
(22) |
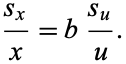 |
(23) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.
Bevington, P. R. Data Reduction and Error Analysis for the Physical Sciences. New York: McGraw-Hill, pp. 58-64, 1969.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|