


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-2-2021
Date: 10-1-2016
Date: 24-3-2021
|
There are a number of point processes which are called Hawkes processes and while many of these notions are similar, some are rather different. There are also different formulations for univariate and multivariate point processes.
In some literature, a univariate Hawkes process is defined to be a self-exciting temporal point process 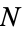 whose conditional intensity function
whose conditional intensity function 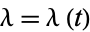 is defined to be
is defined to be
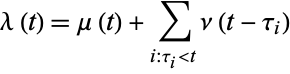 |
(1) |
where 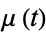 is the background rate of the process
is the background rate of the process 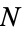 , where
, where 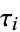 are the points in time occurring prior to time
are the points in time occurring prior to time 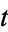 , and where
, and where 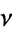 is a function which governs the clustering density of
is a function which governs the clustering density of 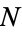 . The function
. The function 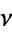 is sometimes called the exciting function or the excitation function of
is sometimes called the exciting function or the excitation function of 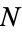 . Similarly, some authors (Merhdad and Zhu 2014) denote the conditional intensity function
. Similarly, some authors (Merhdad and Zhu 2014) denote the conditional intensity function 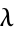 by
by 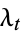 and rewrite the summand in () as
and rewrite the summand in () as
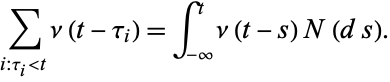 |
(2) |
The processes upon which Hawkes himself made the most progress were univariate self-exciting temporal point processes 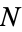 whose conditional intensity function
whose conditional intensity function 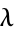 is linear (Hawkes 1971). As a result, some authors refer to such processes as Hawkes processes. In general, however, such
is linear (Hawkes 1971). As a result, some authors refer to such processes as Hawkes processes. In general, however, such 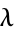 behavior is typically specified, i.e., processes for which
behavior is typically specified, i.e., processes for which 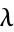 is linear are referred to as linear Hawkes processes and are differentiated from their non-linear counterparts whose conditional intensity functions
is linear are referred to as linear Hawkes processes and are differentiated from their non-linear counterparts whose conditional intensity functions 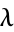 are non-linear (Merhdad and Zhu 2014).
are non-linear (Merhdad and Zhu 2014).
Still other authors consider two alternative brands of univariate Hawkes processes, one the so-called intensity-based Hawkes process and the other the so-called cluster-based version, which are equivalent though are studied in different contexts (Dassios and Zhao 2013). In this case, the intensity-based process is a temporal point process 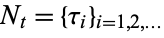 on
on 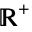 which has a nonnegative exponentially-decaying
which has a nonnegative exponentially-decaying 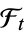 -stochastic intensity
-stochastic intensity 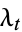 of the form
of the form
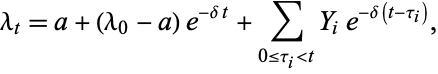 |
(3) |
for 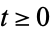 , where
, where 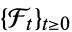 is a history of the process
is a history of the process 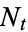 with respect to which
with respect to which 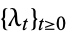 is adapted,
is adapted, 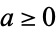 is the constant reversion level,
is the constant reversion level, 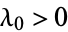 is the initial intensity at time
is the initial intensity at time 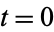 ,
, 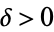 is the constant rate of exponential decay,
is the constant rate of exponential decay,  are the sizes of the self-excited jumps viewed as independent random variables distributed according to some distribution function
are the sizes of the self-excited jumps viewed as independent random variables distributed according to some distribution function 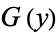 ,
, 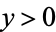 , and
, and 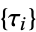 and
and 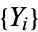 are assumed to be independent of one another. This is equivalent to the cluster-based version in which () is viewed as a marked Poisson cluster process
are assumed to be independent of one another. This is equivalent to the cluster-based version in which () is viewed as a marked Poisson cluster process 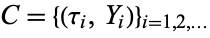 , the only difference being that from the cluster-based perspective:
, the only difference being that from the cluster-based perspective:
1. The set 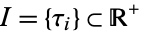 consists of elements known as immigrants which are distributed as an inhomogeneous Poisson process with rate
consists of elements known as immigrants which are distributed as an inhomogeneous Poisson process with rate
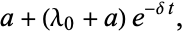 |
(4) |
for 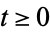 .
.
2. The set 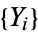 of marks associated to the immigrants
of marks associated to the immigrants 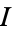 are independent of the immigrants and are distributed as independent random variables according to some distribution
are independent of the immigrants and are distributed as independent random variables according to some distribution 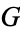 .
.
3. Each immigrant 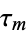 generates a single cluster
generates a single cluster 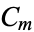 independent of other clusters where here, each
independent of other clusters where here, each 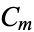 is viewed as a random set subject to a certain branching structure (Dassios and Zhao 2013) which satisfies the property that
is viewed as a random set subject to a certain branching structure (Dassios and Zhao 2013) which satisfies the property that 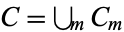 .
.
In addition to these ambiguities, several authors (e.g., Merhdad and Zhu 2014), have made generalized versions of the univariate process described in () which are still referred to as Hawkes processes. One example includes adapting () so that the process has different exciting functions, the result of which is a collection 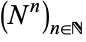 of non-explosive simple point processes for which:
of non-explosive simple point processes for which:
1. 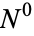 is an inhomogeneous Poisson process with intensity
is an inhomogeneous Poisson process with intensity 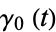 at time
at time 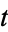 ;
;
2. For every 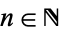 ,
, 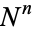 is a simple point process with intensity
is a simple point process with intensity
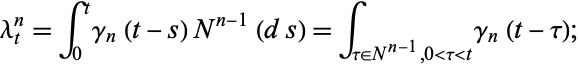 |
(5) |
3. For every 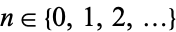 ,
, 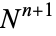 is an inhomogeneous Poisson process with intensity
is an inhomogeneous Poisson process with intensity 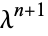 conditional on
conditional on 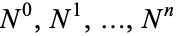 .
.
In this context, the function 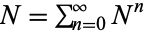 is said to be a univariate Hawkes process with excitation functions
is said to be a univariate Hawkes process with excitation functions 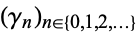 while
while 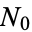 is called the immigrant process and
is called the immigrant process and 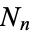 the
the 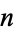 th generation offspring process (Merhdad and Zhu 2014). Note that when
th generation offspring process (Merhdad and Zhu 2014). Note that when 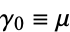 and when
and when 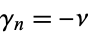 for any
for any 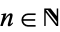 , this extended model reduces to the classical linear model ().
, this extended model reduces to the classical linear model ().
Due to the vast usage of the term Hawkes process among univariate point processes, one expects there to be room for an equally large number of definitions of multivariate Hawkes processes. Surprisingly, however, the most common use of the term is assigned to a relatively straightforward extension of equations () and (), whereby one says that a multivariate 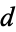 -dimensional counting process
-dimensional counting process 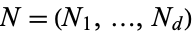 taking values in
taking values in 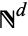 is a multivariate Hawkes process whenever the associated intensity function
is a multivariate Hawkes process whenever the associated intensity function 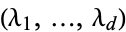 defined by
defined by
![lambda_(i,t)dt=P(N_i has a jump in [t,t+dt]|F_t),](https://mathworld.wolfram.com/images/equations/HawkesProcess/NumberedEquation6.gif) |
(6) |
for 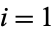 , ...,
, ..., 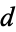 has the form
has the form
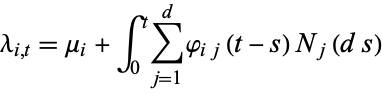 |
(7) |
(Bacry et al. 2012). Here, 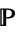 stands for probability,
stands for probability, 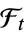 is the sigma-algebra generated by
is the sigma-algebra generated by 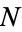 up to present time
up to present time 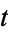 ,
, 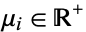 , and
, and 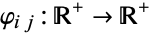 for
for 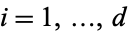 .
.
It is worth noting, however, that precisely as with the univariate case, some authors distinguish between different "types" of multivariate Hawkes processes (Liniger 2009) while other authors define completely separate types of multivariate functions to be multivariate Hawkes processes (Carlsson et al. 2007).
REFERENCES:
Bacry, E.; Delattre, S.; Hoffmann, M.; and Muzy, J. F. "Scaling Limits for Hawkes Processes and Applications to Financial Statistics." 2012. https://arxiv.org/abs/1202.0842v1.
Carlsson, J.; Foo, M. C.; Lee, H. H.; and Shek, H. "High Frequency Trade Prediction with Bivariate Hawkes Process." 2007. https://users.iems.northwestern.edu/~armbruster/2007msande444/report1b.pdf.
Dassios, A. and Zhao, H. "Exact Simulation of Hawkes Process with Exponentially Decaying Intensity." Electron. Commun. Probab. 18, 1-13, 2013.
Hawkes, A. G. "Spectra of Some Self-Exciting and Mutually Exciting Point Processes." Biometrika 58, 83-90, 1971.
Hawkes, A. G. and Oakes, D. "A Cluster Process Representation of a Self-Exciting Process." J. Appl. Prob. 11, 493-503, 1974.
Hawkes, A. G. and Adamopoulos, L. "Cluster Models for Earthquakes: Regional Comparisons." Bull. Int. Statist. Inst. 45, 454-461, 1973.
Liniger, T. "Multivariate Hawkes Processes." 2009.
Mehrdad, B. and Zhu, L. "On the Hawkes Process with Different Exciting Functions." 2014. https://arxiv.org/abs/1403.0994v1.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
العتبة العباسية تستعدّ لتكريم عددٍ من الطالبات المرتديات للعباءة الزينبية في جامعات كركوك
|
|
|